NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Arithmétique
Débutants Opérations	MODULO					Glossaire Nombres
INDEX Théorie des nombres	Introduction	Théorie		Propriétés	Formulaire
	Applications	Calculs		Carrés	Cubes
	Jeux	Sun Zi		Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7		Log Modulaire	11^10 = 32 mod 71
	Classes de congruence		Triangle des modulos
		Sommaire de cette page >>> Modulo et résidus >>> Congruences >>> Classes de congruences

CONGRUENCES

Modulo & Résidus

En arithmétique modulaire, c'est le reste de la division qui devient la vedette !

Dans cette arithmétique utilisant les congruences, le but est plutôt de rechercher des divisibilités. La quantité de restes d'une division par k étant limitée, l'étude d'une propriété est réduite à l'analyse d'un nombre limité de cas.

Pour se familiariser avec la notion de modulo, on lira préalablement Approche ou, l'arithmétique de l'horloger.

En bref

Voir Le nombre 763 est un nombre modeste / Division euclidienne

MODULO ET RÉSIDUS

Division de a par m

Lorsqu'on effectue une division a / m

On peut toujours écrire cette division sous la forme suivante:

a = k .m + b

Ici, dans le monde des modulos, on s'intéressera plutôt à la valeur du reste b et moins à celle du quotient k.

Vocabulaire

Deux mots de jargon qui veulent dire:

Modulo m : je divise par m;

Résidu  b : le reste b de cette division.

Exemples: Modulo successifs de 35

Classique		Monde des modulos
a =	k . m + b	Modulo a (mod m)	Résidu b
35 =	17 x 2 + 1	35 mod 2	= 1
	11 x 3 + 2	35 mod 3	= 2
	8 x 4 + 3	35 mod 4	= 3
	7 x 5 + 0	35 mod 5	= 0
	5 x 6 + 5	35 mod 6	= 5
	5 x 7 + 0	35 mod 7	= 0

Dans le monde du modulo, on ne s'intéresse pas au quotient k.

Notations: toutes ces expressions signifient la même chose

On trouve aussi ces notations:

Observations

a (mod m) pour a et m jusqu'à 10

m	a
	1	2	3	4	5	6	7	8	9	10
1	0	0	0	0	0	0	0	0	0	0
2	1	0	1	0	1	0	1	0	1	0
3	1	2	0	1	2	0	1	2	0	1
4	1	2	3	0	1	2	3	0	1	2
5	1	2	3	4	0	1	2	3	4	0
6	1	2	3	4	5	0	1	2	3	4
7	1	2	3	4	5	6	0	1	2	3
8	1	2	3	4	5	6	7	0	1	2
9	1	2	3	4	5	6	7	8	0	1
10	1	2	3	4	5	6	7	8	9	0

En bleu, résidu > 4

Notez: le résidu n'est jamais supérieur à m, évidemment !

a (mod m) pour a à partir de 17 et m jusqu'à 17

m	a
	17	18	19	20	21	22	23	24	25	26
1	0	0	0	0	0	0	0	0	0	0
2	1	0	1	0	1	0	1	0	1	0
3	2	0	1	2	0	1	2	0	1	2
4	1	2	3	0	1	2	3	0	1	2
5	2	3	4	0	1	2	3	4	0	1
6	5	0	1	2	3	4	5	0	1	2
7	3	4	5	6	0	1	2	3	4	5
8	1	2	3	4	5	6	7	0	1	2
9	8	0	1	2	3	4	5	6	7	8
10	7	8	9	0	1	2	3	4	5	6
11	6	7	8	9	10	0	1	2	3	4
12	5	6	7	8	9	10	11	0	1	2
13	4	5	6	7	8	9	10	11	12	0
14	3	4	5	6	7	8	9	10	11	12
15	2	3	4	5	6	7	8	9	10	11
16	1	2	3	4	5	6	7	8	9	10
17	0	1	2	3	4	5	6	7	8	9

En bleu, résidu > 7

Coin maths

CONGRUENCES

Formulation

Dans

a = k .m + b

a est congru à b modulo m

On écrit

a b (mod m)

Exemple

a = k .m + b	a b (mod 3)
35 = 11 x 3 + 2	35 2 (mod 3)
36 = 12 x 3 + 0	36 0 (mod 3)
37 = 12 x 3 + 1	37 1 (mod 3)
38 = 12 x 3 + 2	38 2 (mod 3)

Il est équivalent de dire:

a = k . m + b	a divisé par m produit un reste b
a – b = k . m	a et b ont même reste lorsque divisé par m
	a – b est divisible par m
	a – b est multiple de m
a b (mod m)	a et b sont congrus modulo m
	a est congru à b modulo m

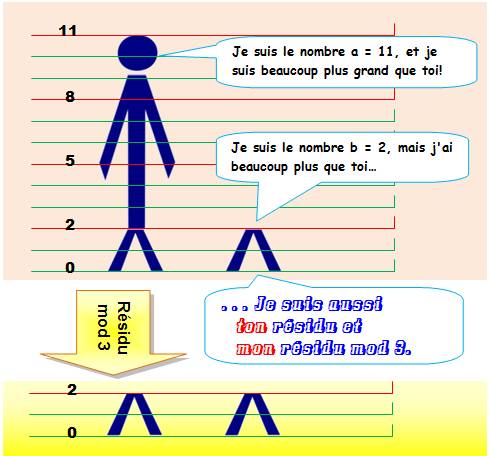
Illustration où il est montré que b joue un double jeu: le nombre b et le reste b

Merci à Mohamed Biby

Notez

(35, 2), (38, 2), (41, 2) et (44, 2)

Sont quatre couples ayant un air de famille.

Tous ces nombres sont congrus modulo 3.

On obtient le même reste en les divisant par 3.

On a créé une race (classe) de nombres partageant la même propriété.

CLASSES DE CONGRUENCES

Classes

Avec la congruence

modulo m donnée,

on partage les nombres

en plusieurs classes.

Notez

Le nombre de classes

est égal à m,

l'argument du modulo

Nombres divisibles par 1

n =	1	2	3	4	5	6	7	8	9	10
mod 1	0	0	0	0	0	0	0	0	0	0

Ils le sont tous = > 1 seule classe

Nombres divisibles par 2

n =	1	2	3	4	5	6	7	8	9	10
mod 2	1	0	1	0	1	0	1	0	1	0

Il y a ceux qui le sont et ceux qui ne le sont pas

Soit pairs et impairs = > 2 classes

Nombres divisibles par 3

n =	1	2	3	4	5	6	7	8	9	10
mod 3	1	2	0	1	2	0	1	2	0	1

Ils sont de trois sortes:

nombres ayant pour reste 0, 1 ou 2

0 3 6 9 (mod 3)

1 4 7 10 (mod 3)

2 5 8 11 (mod 3)

=> 3 classes

Coin maths

Suite Retour	Carrés modulo 4 et 8 Approche Groupe des entiers modulo 4 avec addition (Z4) Tour de magie avec les modulos
Congruence	Voir en tête Clé de divisibilité, une application de la théorie du modulo Log Modulaire Nombres congruents Résidus quadratiques Application à la puissance 11 Congruence avec trigonométrie
Voir	Application à la factorisation Calcul mental – Index Divisibilité Exemple d'application du modulo en Codage RSA Fractions et horloges Géométrie – Index La division Nombres Cycliques Nombres de Carmichaël Nombres Premiers Nombres Rationnels Preuve par 9 – Glossaire Pseudo Premiers Pseudo Premiers Absolus Théorie des nombres – Index
Diconombre	Nombre 105
Livre	Algèbre 1 – Cours et 600 exercices corrigés – 1^re année MPSI, PCSI, PTSI – Jean-Marie Monier – Dunod – 1996
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Modulo.htm