|
|||||||||||||||||||||||||||
![]()
|
PETIT THÉORÈME DE FERMAT Ce théorème dit que
D = a p–1 – 1 est divisible par p sous certaines
conditions. Explorons ces
conditions. Notion de pseudo-premier. |
|
|
||||||||||||
|
Rappel du petit théorème de Fermat (PTF) (1) - Si p est un nombre premier;
(2) - Si a et p
sont premiers entre eux; (3) - Alors, D = a p –1 – 1 est
divisible par p. Exemple Que
dire de 1713 ? Voir Magie
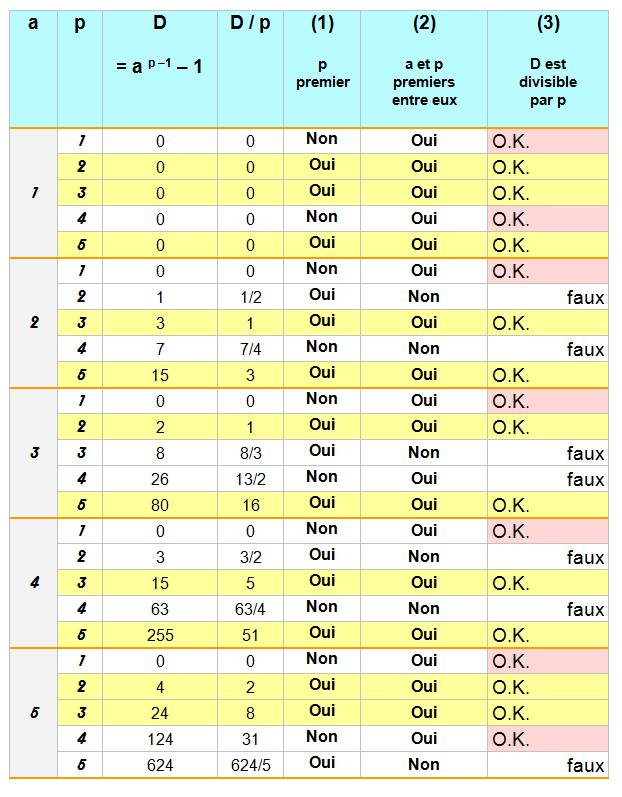
du PTF Méthode On calcule D
= a p –1 – 1 pour
a et p jusqu'à 5. On
donne aussi la valeur de la division D / p On
donne l'état des 3 conditions indiquées dans le théorème (1), (2) et (3) Fermat
dit: (1) et (2) => (3) Rangées
en jaune
Exemple de lecture Théorème de Fermat
vérifié (deux dernières rangées en jaune)
Contre exemple (dernière
case en rose)
Les autres cases roses sont triviales, car elles
correspondent à n = 0 |
||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2
p – 1
(1) - Si p est
un nombre premier;
(2) - Si a et p sont premiers entre eux. Exploration pour p
premier ou non
Le
théorème est vérifié: le résidu est bien 1 pour les nombres premiers
La
réciproque n'est pas vraie pour 341. Il existe donc des nombres
composés qui vérifient le test de Fermat: le résidu est 1 et p n'est
pas premier. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Pour
a = 2: 341, 561,
645, 1105, 1387 … Pour
a = 3: 91, 121,
286, 671, 703 … Pour
a = 4: 15, 85,
91, 341, 435 … |
|
Voir suite
en Pseudo Premiers / Probablement premier
![]()
|
Suite |
Le petit théorème de Fermat |
|
Voir |
|
|
Avancé |
Voir
un sujet complet utilisant ces notions: On y
verra en particulier le cas de la puissance 15 |
|
Découvrir |
|
|
Cette page |
![]()