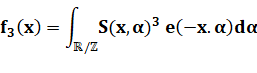|
|||||||||||||||||||||||||||||||||||||||
![]()
|
CONJECTURE DE GOLDBACH Début de preuve ? Les axes de recherche: des
plus simples aux plus sophistiquées. En
2013, le
mathématicien
Harald Helfgott publie la démonstration de la conjecture
faible: tout nombre est somme de trois premiers.
Tao Terence est sur la piste de conjecture forte: tout nombre pair est la somme de cinq nombres premiers. La
conjecture dit: trois. |
Voir Helfgott et le crible
d'Ératosthène
Théorème
d'Helfgott (conjecture ternaire de Goldbach)
et sa
conséquence pour les nombre pairs

Conjecture
forte (ou binaire) de Goldbach

![]()
|
|
||
|
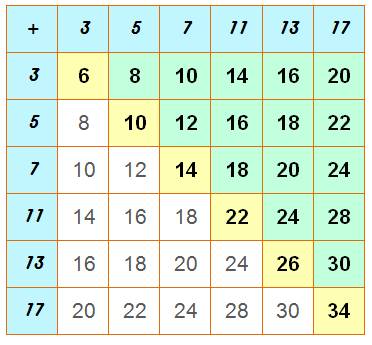
QT = k(k+1) /2 =
21
QP = P – 3 = 14
QPAIR
< QTABLE |
Quels
sont les nombres pairs produits? 61,
81, 102, 121, 142, 162,
182, 202, 222, 242, 261,
281, 301, 320, 341. Soit
21 nombres dont 14 distincts. À noter que la table ne donne pas le 32 qui viendra en ajoutant les
nombres premiers suivants. |
|
|
Conclusions La
table offre potentiellement suffisamment de place pour recevoir tous les
nombres pairs. Cependant, certains sont produits plusieurs fois. Cette
redondance n'est pas gage de complétude. La preuve s'envole … Certains
ont néanmoins poursuivi cette approche
en appelant les probabilités sans conclure vraiment. Principal
écueil: pour des nombres très, très grands, existe-il des nombres premiers
suffisamment proches pour donner toute la séquence des nombres pairs? |
||
|
Si
n = P1 + P2, la quantité de nombres premiers
entre 0 et n est voisine de n / ln (n) - (Théorème des nombres premiers
établi par Gauss en 1792). On en déduit
qu'il existe en moyenne environ n / 2ln² (n) façons d'écrire un entier n pair
assez grand comme somme de deux premiers. Une proportion importante de
nombres pairs est somme de deux nombres premiers impairs. Plus n augmente et
plus la probabilité est grande de trouver deux nombres premiers qui
correspondent. À partir de ce constat, certains tentent de progresser vers la
résolution de la conjecture. Sans succès reconnu à ce jour.
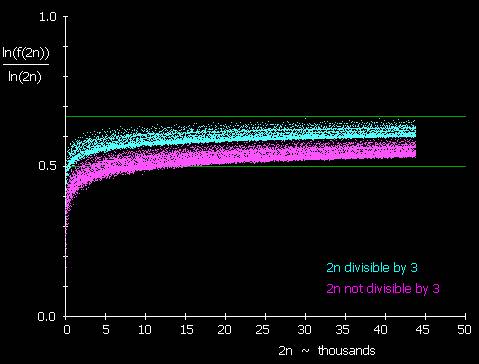
Image extraite de Evidence for Goldbach
par Kevin Brown |
Voir Comète
de Goldbach
|
|
||
|
Comète de Goldbach |
Observation: la quantité de partitions d'un nombre pair en somme de deux premiers
croit lorsque n croit. Allure: Le graphe qui représente cette
quantité en fonction de n présente une allure de comète. Deux bandes se
détachent se propageant asymptotiquement, semble-t-il, vers la droite. Espoir: Peut-on en déduire certaines propriétés qui mèneraient à la
résolution de la conjecture? |
|
|
Somme minimale |
Espoir sur la fonction qui à tout
nombre premier p associe la valeur Sp, plus petit entier pair n admettant une
partition de Goldbach contenant p mais aucune partition de Goldbach avec un
nombre premier plus petit que p. Bien que rien à ce sujet ne soit
encore prouvé, l'allure du graphe de Sp met clairement en relief une
régularité qui ne doit rien au hasard. De nouveaux théorèmes y figurent en
filigrane. Benoît
Rittaud – La Recherche – Janvier 2004 |
|
|
Méthode du cercle Analyse de Fourier sur les entiers |
Méthode analytique. Elle fait appel à des notions
avancées de mathématiques. La somme de premiers est exprimée sous la forme
d'une série
de Fourier s'appliquant sur le cercle
unité. Nous avons à faire à des sommes d'exponentielles. Exemple pour information: la
fonction f3 donnant la quantité de possibilités de sommes de trois
premiers pour un entier x, s'écrit (S étant une certaine somme
d'exponentielles):
avec e(x) = exponentielle complexe = La stratégie de résolution (toute
l'ingéniosité) consiste alors à borner la fonction. Si f3 > 0,
alors la somme triple existe toujours et le problème est résolu. Cette méthode fut introduite par Hardy et Littlewood en 1918 en tant que
fonction de partition impliquée dans les sommes
de carrés. Sont aussi impliquées: l'hypothèse de Riemann, la
fonction L de Dirichlet … (La fonction L est une cousine de la fonction zêta) Suite >>> Crible d'Helfgott >>> Cercles d'Apollonius >>> |
|
|
Méthode du crible (sieve method) |
Méthode combinatoire
issue du crible
d'Ératosthène Méthode, envisagée par Adrien-Marie
Legendre (1808), utilisée en 1919 par Brun qui démontre que tout grand nombre
pair est la somme de deux nombres, chacun ayant au maximum neuf facteurs
premiers. Méthode améliorée par Selberg en
1947. Cette méthode met en jeu deux ensembles
de nombres décrits par des inégalités et faisant appel à la théorie combinatoire. Construire les deux
ensembles est la majeure difficulté de la méthode. "Brun réussit à montrer que
r(n), le nombre de façons d'écrire n comme somme de deux premiers, est
inférieur à 8 R(n) où R(n) est la fonction asymptotique conjecturée pour r(n)
si n est grand. Etc." La suite est à lire dans la revue citée |
|
|
|
||
|
En 2016, Harald Helfgott a développé
un crible performant en utilisant la méthode du cercle
et économisant la mémoire en passant d'une taille N à la taille racine
cubique de N. Exemple pour
écrire les recherche des nombres premiers jusqu'à n = 1 000 000, il faut 200
rames de papiers et avec cette méthode 60 feuilles suffisent (200 000 ^1/3 =
58,48…) Motivation d'Helfgott: nécessité
d'avoir ce résultat pour prouver la conjecture ternaire de Goldbach (Impair =
P1 + P2 + P3). |
La méthode fournit à la fois les
nombres premiers consécutifs et aussi la factorisation des autres nombres: et
même le calcul de fonctions arithmétiques (Moebius, Liouville …), comme le
permet d'ailleurs le crible d'Ératosthène. Cette remarque tient au
fait que de nombreuses améliorations ont été apportées au crible initial,
mais focalisées sur la recherche des nombres premiers. |
|
|
Techniques utilisées Elles
dépassent le cadre de ces présentes pages (niveau supérieur). L'auteur
cite: Approximation diophantienne combinée
à une approximation linéaire locale. Travaux de Dirichlet, Sierpinski et
de Voronoï. |
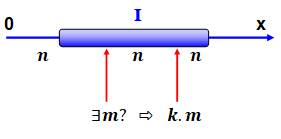
Exemple de recherche
Soit I un
intervalle (n – delta n à n + delta n) appartenant à (0,x). Comment trouver les entiers m tels
que, au moins un de ses multiples, soit dans l'intervalle ? |
|
|
|
|
|
Tout entier impair
est somme de cinq nombres premiers au plus. O = P + P
+ P + P + P Sa démonstration s'appuie sur la vérification que tous
les entiers pairs jusqu'à 1014 sont somme d'au plus deux nombres
premiers. Nous avons prouvé que tout nombre
impair N plus grand que 1 peut être
exprimé comme la somme de, au plus, cinq nombres premiers, améliorant le
résultat de Ramaré qui dit que tout nombre entier pair
est la somme d'au plus six nombres premiers. Nous avons utilisé la méthode du cercle de Hardy-Littlewood et Vinogradov et également
l'identité de Vaughan. Extrait et traduction
de l'abstract de son article.
Il reste des termes dans la
décomposition dont nous ne pouvons rien dire. La bonne méthode reste à
trouver.
Voir revue citée.
Sa démonstration fait appel à des vérifications par
ordinateurs, très exigeantes en puissance de calcul et à un algorithme seulement disponible
depuis 2011 (David Platt). La conjecture faible de Goldbach
(ternary Goldbach conjecture) dit que tout nombre impair
supérieur ou égal à 7 est la somme de trois nombres premiers. Hardy et
Littlewood en 1923 utilisaient les estimations de certaines séries de
Fourrier et de leurs sommes. Ici, nous montrons comment estimer de telles
séries (…). Ceci fait partie intégrante de la preuve par l'auteur de la
conjecture faible. Extrait et traduction
de l'abstract de son article.
Ramener le calcul du nombre de
représentations d'un entier n impair comme somme de trois nombres premiers à
celui d'une intégrale sur l'ensemble des entiers
qu'on aurait au préalable "enroulé" sur
un cercle, faisant coïncider à chaque tour les réels x, x+1, x+2 …. En
coupant cette intégrale en deux, sur les arcs majeurs et mineurs, on doit
prouver qu'elle est positive, et donc qu'il y a au moins une façon d'écrire n
comme somme de trois nombres premiers. Extrait de Tangente –
Juillet-août 2013 – Goldbach, une conjecture résistante par Élisabeth Busser
- page 23 |
|
Voir Actualités
|
Le théorème du perroquet Le théorème du perroquet:
roman (1998) de Denis Guedj (1940-2010). Un mathématicien aux confins de
l'Amazonie aurait démontré la conjecture. Oncle
Petros et la conjecture de Goldbach: roman d'Apóstolos
Doxiádis (né en 1953) paru en 1992. Histoire d'un chercheur fictif précoce,
occasion pour l'auteur de raconter l'histoire de mathématiciens célèbres. |
Voir Romans
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Revue |
|
|
|
|
|
Cette page |
![]()