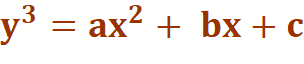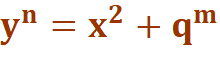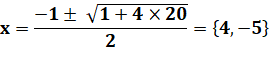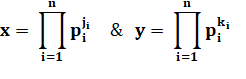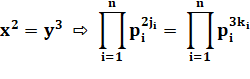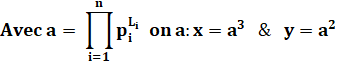|
Édition du: 03/11/2021 |
|
INDEX |
Équations DIOPHANTIENNES |
|||
|
Équation en y3 |
||||
![]()
|
Équations diophantiennes en
Expressions
diophantiennes du deuxième degré dont les valeurs sont les cubes de nombres
entiers. Il s'agit donc de trouver quand un polynôme du deuxième degré est
égal à un cube. |
||
|
|
Sommaire de cette page >>> Approche >>> Solution >>> Cas de yn = x2 + qm >>> Cas de y3 = x2 >>> Bilan |
Débutants Glossaire Équations
du 2e degré |
|
Formation d'une relation en y3 Étude de
l'équation:
Calcul
des racines
de l'équation: En faisant apparaitre un cube:
Cette relation est satisfaite pour x =
Cette relation est satisfaite pour x = |
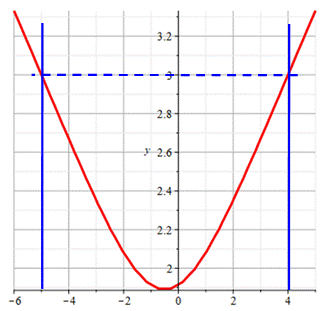
Graphe de y3 = x² + x + 7
|
||
|
Formalisation (Évidente !) |
Si ax² +
bx + c = 0 pour x1 et x2, |
||
|
Exemple
|
x² + x – 20 + 103 x= 4 => 16 + 4 – 20 + 1000 = 1000 = 103 |
||
|
Les 148 solutions pour a, b, c, x
jusqu'à 10. Il y en a 65 752 jusqu'à 100. |
||||
|
a, b, c, x, y3,
y 1,
1, 2, 2, 8, 2 1,
1, 6, 1, 8, 2 1, 1, 7, 4, 27, 3 1,
1, 8, 7, 64, 4 1,
2, 1, 7, 64, 4 1,
2, 3, 4, 27, 3 1,
2, 5, 1, 8, 2 1,
2, 5, 10, 125, 5 1,
3, 4, 1, 8, 2 1,
3, 9, 3, 27, 3 1,
3, 10, 6, 64, 4 1,
4, 3, 1, 8, 2 1,
4, 4, 6, 64, 4 1,
4, 6, 3, 27, 3 1,
4, 8, 9, 125, 5 1,
5, 2, 1, 8, 2 1,
5, 3, 3, 27, 3 1,
6, 1, 1, 8, 2 1,
6, 9, 5, 64, 4 1,
7, 4, 5, 64, 4 1,
7, 5, 8, 125, 5 1,
7, 9, 2, 27, 3 1,
8, 7, 2, 27, 3 1,
9, 5, 2, 27, 3 1,
10, 3, 2, 27, 3 1,
10, 6, 7, 125, 5 1,
10, 8, 4, 64, 4 2,
1, 5, 1, 8, 2 2,
1, 6, 3, 27, 3 2,
1, 6, 10, 216, 6 2,
1, 9, 5, 64, 4 2,
2, 3, 3, 27, 3 2,
2, 4, 1, 8, 2 2,
2, 4, 5, 64, 4 2,
3, 3, 1, 8, 2 2,
3, 6, 7, 125, 5 2,
4, 2, 1, 8, 2 |
2,
5, 1, 1, 8, 2 2,
5, 9, 2, 27, 3 2,
5, 9, 9, 216, 6 2,
6, 7, 2, 27, 3 2,
6, 8, 4, 64, 4 2,
7, 4, 4, 64, 4 2,
7, 5, 2, 27, 3 2,
8, 3, 2, 27, 3 2,
8, 5, 6, 125, 5 2,
9, 1, 2, 27, 3 2,
10, 8, 8, 216, 6 3,
1, 4, 1, 8, 2 3,
2, 3, 1, 8, 2 3,
2, 5, 6, 125, 5 3,
2, 8, 4, 64, 4 3,
2, 8, 8, 216, 6 3,
3, 2, 1, 8, 2 3,
3, 4, 4, 64, 4 3,
3, 9, 2, 27, 3 3,
4, 1, 1, 8, 2 3,
4, 3, 10, 343, 7 3,
4, 7, 2, 27, 3 3,
5, 5, 2, 27, 3 3,
6, 3, 2, 27, 3 3,
7, 1, 2, 27, 3 3,
8, 10, 5, 125, 5 3,
9, 5, 5, 125, 5 3,
9, 6, 7, 216, 6 3,
9, 10, 3, 64, 4 3,
10, 7, 3, 64, 4 3,
10, 10, 9, 343, 7 4,
1, 3, 1, 8, 2 4,
1, 9, 2, 27, 3 4,
1, 10, 9, 343, 7 4,
2, 1, 9, 343, 7 4,
2, 2, 1, 8, 2 4,
2, 6, 7, 216, 6 4,
2, 7, 2, 27, 3 |
4,
3, 1, 1, 8, 2 4,
3, 5, 2, 27, 3 4,
3, 10, 5, 125, 5 4,
4, 3, 2, 27, 3 4,
4, 5, 5, 125, 5 4,
5, 1, 2, 27, 3 4,
6, 10, 3, 64, 4 4,
7, 7, 3, 64, 4 4,
8, 4, 3, 64, 4 4,
9, 1, 3, 64, 4 4,
10, 7, 8, 343, 7 5,
1, 2, 1, 8, 2 5,
1, 2, 10, 512, 8 5,
1, 5, 2, 27, 3 5,
2, 1, 1, 8, 2 5,
2, 3, 2, 27, 3 5,
2, 7, 8, 343, 7 5,
3, 1, 2, 27, 3 5,
3, 10, 3, 64, 4 5,
4, 7, 3, 64, 4 5,
5, 4, 3, 64, 4 5,
5, 6, 6, 216, 6 5,
6, 1, 3, 64, 4 5,
9, 9, 4, 125, 5 5,
10, 5, 4, 125, 5 6,
1, 1, 1, 8, 2 6,
1, 1, 2, 27, 3 6,
1, 7, 3, 64, 4 6,
2, 4, 3, 64, 4 6,
2, 8, 9, 512, 8 6,
3, 1, 3, 64, 4 6,
5, 9, 4, 125, 5 6,
6, 5, 4, 125, 5 6,
6, 7, 7, 343, 7 6,
7, 1, 4, 125, 5 7,
1, 9, 4, 125, 5 7,
2, 5, 4, 125, 5 |
7,
2, 9, 10, 729, 9 7,
3, 1, 4, 125, 5 7,
7, 6, 5, 216, 6 7,
7, 8, 8, 512, 8 7,
8, 1, 5, 216, 6 7,
10, 10, 1, 27, 3 8,
2, 6, 5, 216, 6 8,
3, 1, 5, 216, 6 8,
8, 7, 6, 343, 7 8,
8, 9, 9, 729, 9 8,
9, 1, 6, 343, 7 8,
9, 10, 1, 27, 3 8,
10, 9, 1, 27, 3 9,
2, 7, 6, 343, 7 9,
3, 1, 6, 343, 7 9,
8, 10, 1, 27, 3 9,
9, 8, 7, 512, 8 9,
9, 9, 1, 27, 3 9,
9, 10, 2, 64, 4 9,
9, 10, 10, 1000, 10 9,
10, 1, 7, 512, 8 9,
10, 8, 1, 27, 3 9,
10, 8, 2, 64, 4 10,
2, 8, 7, 512, 8 10,
3, 1, 7, 512, 8 10,
7, 10, 1, 27, 3 10,
7, 10, 2, 64, 4 10,
8, 8, 2, 64, 4 10,
8, 9, 1, 27, 3 10,
9, 6, 2, 64, 4 10,
9, 8, 1, 27, 3 10,
9, 8, 3, 125, 5 10,
10, 4, 2, 64, 4 10,
10, 5, 3, 125, 5 10,
10, 7, 1, 27, 3 10,
10, 9, 8, 729, 9 |
|
|
Arif et
Abu Muriefah ont prouvé qu'il n'existe que trois solutions pour : Une exploration par ordinateur contredit cette affirmation
et me donne quatorze solutions. En voici deux exemples avec 88². |
|
|
|
Arif et Abu
Muriefah, Luca et Tao ont prouvé qu'il n'existe que deux solutions pour : Je confirme. |
|
|
|
Luca a
trouvé les solutions primitives de: |
|
|
|
Bugeaud,
Mignotte et Siksek ont trouvé toute les solutions de: Soit une
puissance éloignée d'un carré d'une valeur 7. |
|
|
Les solutions pour x, y jusqu'à1000 et n et m jusqu'à 20
et q jusqu'à 100
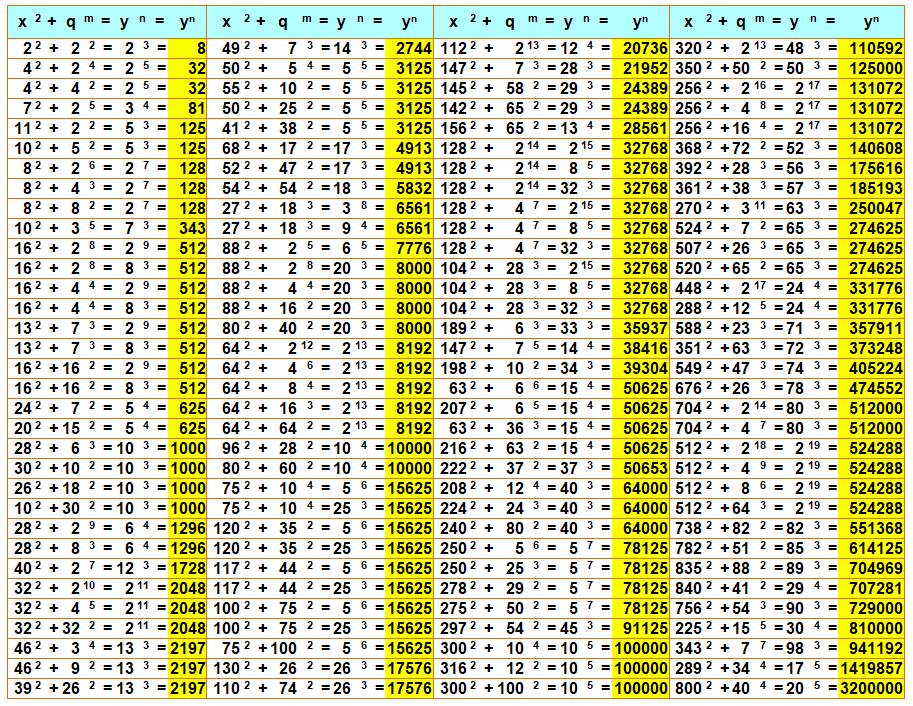
|
Seule
solution |
x = a3 et y = a2 |
|
|
Démonstration Décomposition en facteurs premiers de chacun des
nombres x et y Écriture de l'équation avec ces développements. Théorème
fondamental de l'arithmétique: les exposants sont égaux. |
|
|
|
Propriétés Pour chacune des
solutions proposées, il existe une infinité de solutions à la relation: y3
= ax² + bx + c. Nouvel
exemple
avec la dernière solution citée: 10,
10, 9, 8, 729, 9. 10x² + 10x + 9 – 729 + k3 = k3 pour x = 8 k = 2 => 10 x 64 + 10 x 8 + 9 – 729 + 8
= 0 + 8 = 23 Les
mathématiciens se sont intéressés à des cas particuliers de cette équation et
on trouvé quelques solutions. (Voir
la rérence) Note Voir l'expression voisine: y2 =
x3 + k, l'équation de
Mordell. Le mathématicien Louis
Mordell y consacra une bonne partie de son temps. |
Merci à J. Paul Blanc pour l'idée de cette
page
![]()
|
Retour |
|
|
Suite |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/ThNbDemo/aaaDioph/Equay3x2.htm
|