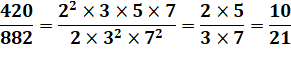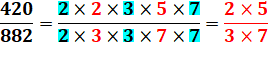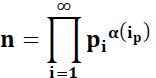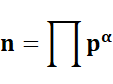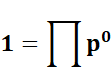|
|||||||||||||||||||||||||||||||||||
![]()
|
Théorème FONDAMENTAL de l’ARITHMÉTIQUE La factorisation
de tout nombre entier n > 1 en produit de nombres premiers est unique, à la permutation des facteurs près. Deux démonstrations
relativement simples à comprendre pour un théorème aussi important! THE FUNDAMENTAL THEOREM OF ARITHMETIC or the unique factorization theorem The
factoring of any integer n > 1 into primes is unique apart
from the order of the prime factors. |
Voir Théorème
fondamental de l'algèbre
Formulation alternative
|
Tout nombre peut être exprimé comme produit unique d'un multiensemble de nombres
premiers. Every
positive integer can be uniquely expressed as the product of a multiset of
primes.
|
Petite
introduction pour novices (niveau collège)
|
Factorisation |
|
|
|
La
décomposition en produits de facteurs premiers consiste à trouver les
produits successifs auxquels est égal ce nombre jusqu'à ne plus pouvoir
trouver d'autres produits. On
procède en cherchant sa divisibilité par les nombres premiers successifs: 2,
3, 5, 7, 11, 13 … |
Exemples 10 = 2 x 5 11 = 11 nombre premier 12 = 2 x 6 = 2 x 2 x 3 24 = 2 x 12 = 2 x 3 x 4 = 2 x 3
x 2 x 2 = 23 x 3 100 = 2 x 50 = 2 x 2 x 25 = 2 x 2 x 5 x 5 111 = 3 x 37 |
|
|
Exemple 420 |
420 = 2 x 210 = 2 x 2 x 105 = 2 x 2 x 5 x 21 = 2² x 5 x 3 x 7 = 2² x 3 x 5 x 7 |
|
|
Exemple 882 |
882 = 2 x 441 On teste la divisibilité de 441 par 3: la somme des chiffres 4 + 4 + 1
= 9, ce nombre est donc divisible par 9 = 3² 882 = 2 x 3² x 49 On reconnait 49 = 7 x 7 882 = 2 x 3² x 7² |
|
|
Application à la simplification de fraction |
|
|
|
Simplification
développée pour
info |
|
|
![]()
|
|
|||
|
|
N = P1.
P2... PR |
=
Q1. Q2... QS |
|
|
|
n = p1.
p2... pr |
=
q1. q2... qs |
|
|
|
pi |
|
|
|
|
p1 |
|
|
|
|
Si p est
premier et p |
alors p |
|
|
|
Contradiction |
hypothèse fausse |
|
|
Rappel notation Le trait vertical veut dire "divise" ;
le trait barré veut dire "ne divise pas". Le trait vertical s'obtient avec la police
symbole; pour le trait barré, utilisez le même symbole en format - police
barrée. Voir Notations |
|||
|
|
|||
|
|
n = p1.
p2... pr |
=
q1. q2... qs |
|
|
A) Nous allons montrer
que les facteurs de chaque côté sont premiers entre eux |
|||
|
|
Si p1 |
=
k.q2 |
|
|
En divisant l’égalité par q2 |
n = k.q2. p2... pr
m = k. p2... pr |
=
q1. q2 .q3...
qs =
q1. q3... qs |
|
|
|
n
|
= q2 .
m > m |
|
|
Or m est plus petit que n. Il existe un plus petit que n qui
admet deux factorisations. |
Contradiction |
hypothèse
fausse |
|
|
B) Nous allons forger
un nouveau nombre pour continuer la démonstration |
|||
|
|
p1 |
<
q1 |
|
|
|
N = (q1
– p1) |
.
(q2.q3 ... qs) |
|
|
Constats :
|
n =
q1 N = (q1
– p1) N |
.
q2.q3 ... qs .
q2.q3 ... qs <
n |
|
|
|
N
n’admet qu’une seule factorisation |
||
|
|
p1 |
|
|
|
Théorème |
Si a |
alors a |
|
|
|
p1 |
|
|
|
|
N = q1.q2.q3 ... qs N = p1.p2.p3...
pr N = p1.(p2.p3...
pr |
– p1.q2.q3
... qs – p1.q2.q3
... qs – q2.q3
... qs) |
|
|
C) Pour finir |
|||
|
p1 ne divise pas (q1 – p1) ni les autres facteurs en q
|
N = p1 .p2.p3...
pr – q2.q3 ... qs N = (q1
- p1) . q2.q3
... qs |
||
|
Nouveau
constat:
|
Contradiction |
hypothèse fausse ■ |
|
|
|
||
|
En application du
théorème fondamental de l'arithmétique, il est possible de
donner une formulation générique de tout nombre |
||
|
Exemple numérique Un nombre est exprimé par un produit de
facteurs premiers, chacun porté à une certaine puissance. |
100 = 22 . 52 13 230 = 2 . 33 . 5 . 72 |
|
|
Écriture généralisée Produit de la succession de tous les
nombres premiers. Un facteur premier qui n'est pas utile pour
représenter le nombre initial est mis à 1 tout simplement en élevant ce
nombre premier à la puissance 0. |
13 230 = 21 . 33
. 5 . 72 . 110. 130 … = 21 . 33
. 5 . 72 . 1 . 1… |
|
|
Passage à la
formulation littérale Utilisant du symbole "Pi
majuscule" qui exprime
le produit. Le produit est réalisé sur tous les
premiers successifs p dont le rang est indiqué par ip L'exposant est appelé alpha. Pour chaque premier d'indice ip
, l'exposant est baptisé |
Décomposition
canonique de n en facteurs premiers
On peut aussi dire:
|
|
|
Formulation abrégée La formulation est souvent simplifiée de la
manière suivante: |
|
|
|
Cas particulier Le nombre un est égal à un produit infini
de 1, obtenu en tant que produit de
tous les nombres premiers forcés à 1 en leur appliquant la puissance 0. |
|
|
|
|
||
|
Une application
immédiate consiste à séparer les facteurs pairs des facteurs impairs
dans un nombre. Cette opération est utile dans de nombreuses démonstrations. |
||
|
Soit un nombre qui s'écrit sous la forme
d'u produit: tous les facteurs sont
débarrassés d'un facteur 2 éventuel; ils sont tous regroupés sous la forme
d'une puissance de 2. Tous les facteurs restants sont impairs et
leur produit est impair. Sous sa forme canonique, un nombre est
immédiatement vu comme le produit d'une puissance de 2 et de puissances de
premiers tous impairs. |
N
= 2k . N'Impair Ex: 10 = 2 x 5 360 = 36 x 10 = 4 x 9 x 2 x 5 = 23
x 45 Ex: 360 = 23 . 32 . 5 = 23
x 45 |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()