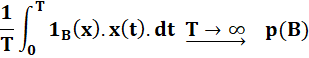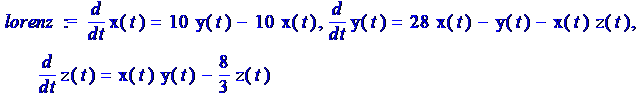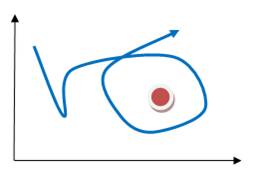
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/08/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Chaos
Débutants Général	Chaos et Attracteurs				Glossaire Général
INDEX Chaos	Chaos	Types d'Attracteurs	Stabilité	Diagramme de phase
		Croissance logistique
		Sommaire de cette page >>> Attracteurs >>> Attracteur étrange de Lorenz >>> Programmation du dessin de l'attracteur

ATTRACTEURS ÉTRANGES

La théorie du chaos affirme que, même si des événements sont divergents, au final et statistiquement, ils s'accumulent sur un noyau de trajectoires nommé attracteur.

ATTRACTEURS
La mécanique est la description du mouvement. Il existe des mouvements fascinants, complexes, proches du hasard. Certains systèmes, dits chaotiques, ont un comportement étrange. Une sorte d'attraction vers un point particulier ou une figure géométrique, un attracteur. Une sorte d'errance au hasard, sans passer deux fois au même endroit, mais sans quitter la figure d'attraction. Ce sont des systèmes dynamiques qui, bien qu'étant en principe déterministes, présentent des comportements complexes, désordonnés en apparence … chaotiques
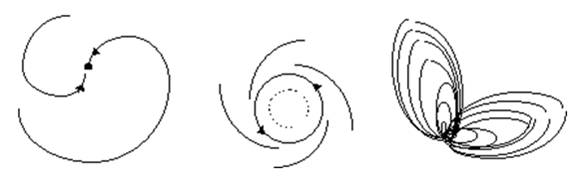
Trois types d'attracteurs Le point fixe Le cycle limite L'attracteur étrange

Voir Attracteur galactique / Lune / Catastrophe

ATTRACTEURS de LORENZ

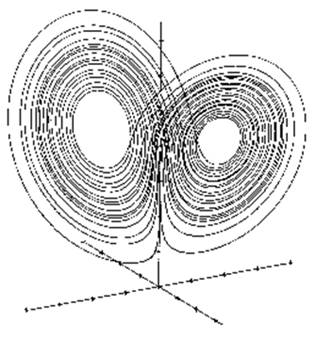
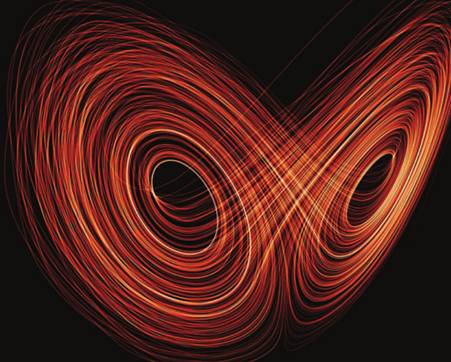
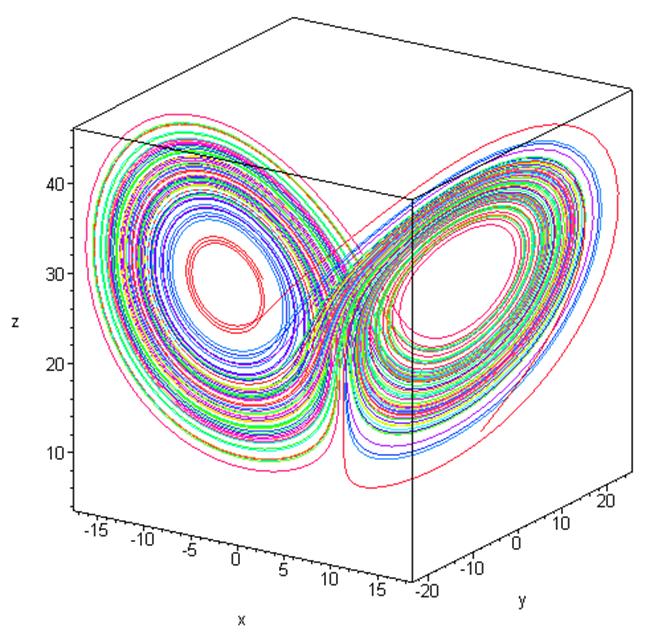
Attracteur étrange

dit de Lorenz

aussi appelé papillon de Lorenz

Équation et courbe

La courbe "papillon de Lorenz" ou courbe de "l'attracteur étrange"

est définie par des équations différentielles:

dx / dt	=	a (y – x)
dy / dt	=	x (b – z) – y
dz / dt	=	xy – cz / d

Ce sont les équations introduites par le météorologiste Edward Lorenz en 1963.
Avec: a = 10 est le nombre de Prandt et b = 8/3, le nombre de Rayleigh. Le rapport c/d est variable. Équations qui n'ont pas de solutions analytique.

Les méthode classiques de résolution montre que les équations nous amènent finallement dans une région limitée. Ce qui siginifie qu'il est suffisant de se concentrer sur les solutions de cette région bornée. Voir Théorie ergodique qui conduit aux résultats importants suivants:

la proportion de temps passé dans la zone bornée converge lorsque le temps tend vers l'infini; et

cette limite est absolument indépendante des conditions initiales.

On est amené à considérer une équation de cette forme

Pour laquelle, au lieu de calculer l'intégrale, il est possible de mesurer des probabilités qui ainsi rensigneront sur le temps passé dans la zone bornée.

Construire l'attracteur avec Maple

Code

with(DEtools):

lorenz :=

diff(x(t),t) = 10*(y(t)-x(t)),

diff(y(t),t) = 28*x(t)-y(t)-x(t)*z(t),

diff(z(t),t) = x(t)*y(t)-8/3*z(t);

DEplot3d({lorenz}, [x(t),y(t),z(t)], t=0..100, stepsize=0.01, [[x(0)=10, y(0)=10, z(0)=10]], orientation=[-35,75], linecolor = t, thickness = 1);

Exécution

Dessin

Note: Vous pouvez reproduire le code dans Maple et vous obtiendrez ce graphique avec la possibilité d'orienter le dessin en interactif avec la souris

Suite	Historique de la théorie du chaos Catastrophes
Voir	Chaos Logistique Complexité Crises des maths Croissance chaotique Fractales Les trois corps Lorenz Lune Notions de la physique moderne Sciences – Index
Sites	L'attracteur étrange de Lorenz Ergodic Theory (Lecture Notes) – Joan Andreu Lazaro Cami - 2010
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Chaos/Attract.htm