|
Ptolémée
(90 - 168)
 Il constate que l'orbite de la Lune se trouve dans un plan incliné de 5°
par rapport au plan zodiacal (Soleil, Terre et autres planètes). La Lune accélère en certains
endroits et décélère en d'autres.
Il constate que l'orbite de la Lune se trouve dans un plan incliné de 5°
par rapport au plan zodiacal (Soleil, Terre et autres planètes). La Lune accélère en certains
endroits et décélère en d'autres.
 Son modèle consistait à faire se déplacer la Lune sur
un cercle (épicycle) dont le centre se déplaçait lui-même sur un petit cercle
centré sur la Terre.
Son modèle consistait à faire se déplacer la Lune sur
un cercle (épicycle) dont le centre se déplaçait lui-même sur un petit cercle
centré sur la Terre.
Nicolas
Copernic (1473-1543)
 Il délogea la Terre de la place centrale et y mit le
Soleil à la place.
Il délogea la Terre de la place centrale et y mit le
Soleil à la place.
Johannes
Kepler (1571-1630) ,
 En utilisant les résultats d'observation de Tycho Brahé (1546-1601), il
perça en 1609 le secret du mouvement des planètes: leur orbite est elliptique.
En utilisant les résultats d'observation de Tycho Brahé (1546-1601), il
perça en 1609 le secret du mouvement des planètes: leur orbite est elliptique.
 Il mit la Lune également sur une orbite elliptique: la
Lune accélère en se rapprochant du Soleil, l'un des foyers de l'ellipse.
Il mit la Lune également sur une orbite elliptique: la
Lune accélère en se rapprochant du Soleil, l'un des foyers de l'ellipse.
 Mais, si les prévisions de position de la Lune
devenaient un peu plus précises, les calculs divergeaient rapidement par
rapport à la réalité.
Mais, si les prévisions de position de la Lune
devenaient un peu plus précises, les calculs divergeaient rapidement par
rapport à la réalité.
Isaac Newton (1642-1727)
 Newton eut l'intuition
géniale de la gravitation
universelle en 1666. Les planètes se déplacent en orbites elliptiques autour
du Soleil parce qu'elles subissent l'influence gravitationnelle de ce
dernier.
Newton eut l'intuition
géniale de la gravitation
universelle en 1666. Les planètes se déplacent en orbites elliptiques autour
du Soleil parce qu'elles subissent l'influence gravitationnelle de ce
dernier.
 Il espère expliquer les irrégularités compliquées et
périodiques de la Lune;
Il espère expliquer les irrégularités compliquées et
périodiques de la Lune;
 Au lieu de rendre la gravité de la Terre seule
responsable du mouvement de la Lune, il tient compte de l'influence
gravitationnelle du Soleil (problème dit des " trois corps "). Seulement ce problème
est très compliqué et, Newton n'a pas pu trouver la solution.
Au lieu de rendre la gravité de la Terre seule
responsable du mouvement de la Lune, il tient compte de l'influence
gravitationnelle du Soleil (problème dit des " trois corps "). Seulement ce problème
est très compliqué et, Newton n'a pas pu trouver la solution.
 Il tente une autre méthode, celle des perturbations. La
trajectoire de la Lune est due principalement à l'influence de la Terre et,
elle est perturbée par le Soleil. Il ne put en venir à bout.
Il tente une autre méthode, celle des perturbations. La
trajectoire de la Lune est due principalement à l'influence de la Terre et,
elle est perturbée par le Soleil. Il ne put en venir à bout.
 Après un an d'efforts, il a atteint 1/6° (0,16°) entre
la réalité et ses calculs.
Après un an d'efforts, il a atteint 1/6° (0,16°) entre
la réalité et ses calculs.
Leonhard
Euler (1707-1783)
Joseph-Louis
de Lagrange (1736-1813)
Pierre-Simon de Laplace (1749-1827)
 Se penchant chacun sur cette question, ils découvrirent
de nouvelles mathématiques, mais la lune refusaient
de se plier à leurs calculs.
Se penchant chacun sur cette question, ils découvrirent
de nouvelles mathématiques, mais la lune refusaient
de se plier à leurs calculs.
 Laplace y passa
40 ans de sa vie et réduisit l'écart à 1/20°
Laplace y passa
40 ans de sa vie et réduisit l'écart à 1/20°
Gustav
Dirichlet (1805-1859)
 En 1858, il pense qu'il a trouvé une nouvelle méthode
pour résoudre les équations de Newton et Il affirme avoir démontré que le système
solaire est stable. Il est mort sans laisser trace de ces démonstrations.
En 1858, il pense qu'il a trouvé une nouvelle méthode
pour résoudre les équations de Newton et Il affirme avoir démontré que le système
solaire est stable. Il est mort sans laisser trace de ces démonstrations.
Henri Poincaré (1854-1912)
 Poincaré proposa une
méthode tout à fait originale et se trouva finalement confronté à la
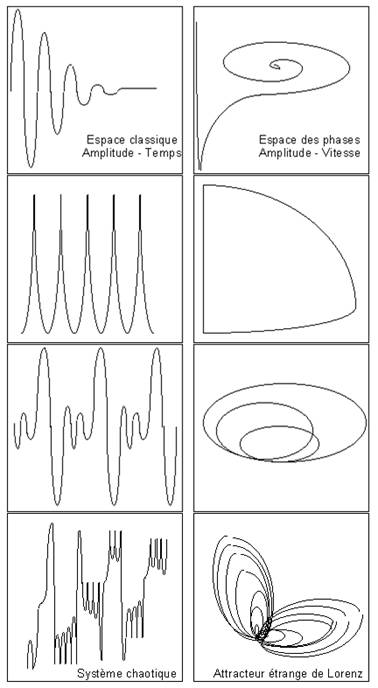
découverte du chaos:
Poincaré proposa une
méthode tout à fait originale et se trouva finalement confronté à la
découverte du chaos:
 La gravité recèle non seulement le régulier et le
prévisible, mais aussi l'irrégulier et le non-prévisible.
La gravité recèle non seulement le régulier et le
prévisible, mais aussi l'irrégulier et le non-prévisible.
 La Lune refusait de se plier aux calculs parce qu'il y
avait dans son comportement une part d'imprévisible!
La Lune refusait de se plier aux calculs parce qu'il y
avait dans son comportement une part d'imprévisible!
 Vouloir s'obstiner à résoudre les équations
différentielles en les développant en série n'est pas la bonne méthode.
Vouloir s'obstiner à résoudre les équations
différentielles en les développant en série n'est pas la bonne méthode.
On fait alors
l'hypothèse que l'état du monde actuel ne dépend que du tout récent passé, sans être influencé par la mémoire
du lointain passé.
 Il faut abandonner la vision de la fourmi limitée à la
touffe d'herbe voisine, et se donner une vision d'aigle survolant les
montagnes et les vallées.
Il faut abandonner la vision de la fourmi limitée à la
touffe d'herbe voisine, et se donner une vision d'aigle survolant les
montagnes et les vallées.
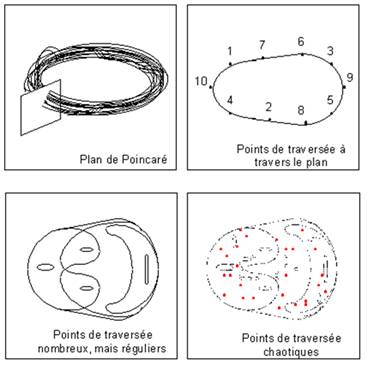
 Poincaré invente une méthode
géométrique allant au-delà de nos trois
dimensions habituelles. On y ajoute trois dimensions de vitesse (espace de
phase), soit six dimensions par objets.
Pour le problème des trois corps (Soleil, Terre et Lune), il faut dix-huit dimensions.
Poincaré invente une méthode
géométrique allant au-delà de nos trois
dimensions habituelles. On y ajoute trois dimensions de vitesse (espace de
phase), soit six dimensions par objets.
Pour le problème des trois corps (Soleil, Terre et Lune), il faut dix-huit dimensions.
 Il montre que l'incertitude est caché
derrière la loi de la gravitation universelle
Il montre que l'incertitude est caché
derrière la loi de la gravitation universelle
 Le système solaire est dominé par la masse du Soleil.
De ce fait, et en première approximation, le mouvement des planètes se déduit
d'un simple problème à deux corps.
Le système solaire est dominé par la masse du Soleil.
De ce fait, et en première approximation, le mouvement des planètes se déduit
d'un simple problème à deux corps.
 Avec deux Soleils et une planète, on aurait un problème
à trois corps et, en prime, le chaos mis en évidence par Poincaré. L'orbite
des planètes aurait été erratique et imprévisible.
Avec deux Soleils et une planète, on aurait un problème
à trois corps et, en prime, le chaos mis en évidence par Poincaré. L'orbite
des planètes aurait été erratique et imprévisible.
|
![]()
![]()
![]()