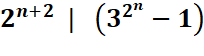NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/03/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
INDEX Divisibilité	Introduction	Par 8	Critères
		Sommaire de cette page >>> Différence de carrés >>> Divisibilité par 8 de N = …cdu >>> Divisibilité par 8 – Critères >>> Divisibilité par une puissance de 2 >>> Forme polynomiale 1 >>> Forme polynomiale 2

DIVISIBILITÉ par 8

Critères de divisibilité et formes polynomiales divisibles.

Un nombre divisible par 8 est terminé par 0, 2, 4, 6 ou 8.

Un carré divisé par 8 a pour reste 0, 1 ou 4.

Le carré d'un nombre impair moins un est divisible par 8.

Voir Règles générales de divisibilité

Différence de carrés
Nombres (n – 2k) et (n + 2k), situés symétriquement par rapport à n	(n + 2k)² – (n – 2k)² = 8 k n
Variante	(n + 3)² – (n – 1)² = 8 n Exemple: n = 7: 10² – 6² = 8 x 7 = 54 = 100 – 36

Voir Divisibilité par 4 / Écarts entre carrés

Divisibilité par 8 de N = …cdu

cdu sont les chiffres des centaines, dizaines et unités. Critère de base Si le nombre cdu est divisible par 8, alors tout nombre de la forme N = …cdu est divisible par 8. Exemples 008 = 8 x 1, 2 008 = 8 x 251, 123 008 = 8 x 15 376 416 = 8 x 52, 2 416 = 8 x 302, 123 416 = 8 x 15 427 Explications N = Mcdu = 1000M + 100c + 10d + u (Voir base décimale) = (8 x 125) M + 100c + 10d + u Le nombre de milliers est divisible par 8, il suffit de vérifier que le reste (cdu) l'est également. Critère amélioré Un nombre est divisible par 8 si 4c + 2d + u est divisible par 8. Exemples 416 => 4 x 4 + 2 x 1 + 6 = 16 + 2 + 6 = 24 = 8 x 3 984 => 4 x 9 + 2 x 8 + 4 = 36 + 16 + 4 = 56 = 8 x 7 Explications cdu = 100c + 10d + u = 96c + 4 c + 8d + 2d + u = 8(12c + d) + 4 c + 2d + u Le premier terme est divisible par 8, il suffit de vérifier que le reste (4c + 2d + u) l'est également. Critère le plus économique en calculs Si c est pair prendre A = 2d + u Si c est impair prendre A = 2d + u + 4 Si A est divisible par 8, alors N est divisible par 8. Exemples 416 => 2 x 1 + 6 = 8 984 => 2 x 8 + 4 + 4 = 24 Explications Avec c = 2k => 4 c + 2d + u = 8k + 2d + u Avec c = 2k + 1 => 4 c + 2d + u = 8k + 4 + 2d + u Le premier terme est divisible par 8, il suffit de vérifier que le reste (2d + u ou 2d + u + 4) l'est également. Le best du best! Prendre cd et ajouter u/2. Si cette somme est divisible par 4, le nombre initial est divisible par 8 Exemples 416 => 41 + 3 = 44 984 => 98 + 2 = 100 Explications cdu = 100c + 10d + u = 8k = 80c + 8d + 20c + 2d + u = 8(10c + d) + 2(10c + d) + u = 8k Le premier terme est divisible par 8, 2(10c + d) + u = 8k 10c + d + u/2 = 4h English corner Numbers are divisible by 8 if the number formed by the last three individual digits is evenly divisible by 8. For example, the last three digits of the number 3624 is 624, which is evenly divisible by 8 so 3624 is evenly divisible by 8.

Voir Divisibilité par 4 avec critères semblables / Brève 438

Retrouver les chiffres manquants

Le nombre x 888 83y est divisible par 72.

Retrouvez les valeurs des chiffres manquants x et y.

72 = 8 x 9; le nombre est donc divisible par 8 et par 9

Divisible par 8 83y est divisible par 8. Essayons: 830/ 8 = 103,75

832 = 104 x 8 et 105 x 8 = 840 y = 2

Divisible par 9 somme des chiffres divisibles par 9.

Alors: x + 8 + 8 + 8 + 8 + 3 + 2 = x + 37.

Le prochain multiple de 9 est 45 et x vaut 8.

En effet: 8 888 832 = 123 456 x 72.

Les procédés correcteurs d'erreurs dans les transmissions fonctionnent sur un principe similaire.

Voir Divisibilité par 9

Divisibilité par une puissance de 2
Divisibilité par 2	N = 10D + u & 2 divise 10	Si 2 divise u
4	N = 100C + du & 4 divise 100	Si 4 divise du
8	N = 1000M + cdu & 8 divise 1000	Si 8 divise cdu
16	N = 10 000N + mcdu & 16 divise 10 000	Si 16 divise mcdu
32	Etc. Pour 2^n	Test sur les n dernier chiffres.

DIVISIBILITÉ PAR 8

de cette forme polynomiale

Théorème

f(n) = 5 ²ⁿ + 7

est divisible par

8

Démonstration

Validation du point de départ
Valeur pour f(1) Le théorème est vrai pour n = 1	f(1)	= 5^2 + 7 = 32 = 8 x 4
Validation de la récurrence
Supposons le théorème vrai pour n	f(n)	= 8 .k
Calculons la valeur pour n+1 Sortons la puissance 2 Faisons 25 = 24 + 1	f(n+1)	= 5^2(n + 1) + 7 = 5² . 5^2n + 7 = 5² . 5^2n + 7 = 24 . 5^2n + 5^2n + 7
En utilisant notre hypothèse	f(n+1)	= 24 . 5^2n + 5^2n + 7 = 24 . 5^2n + f(n) = 24 . 5^2n + 8 . k
Mettons en facteurs f(n+1) est divisible par 8	f(n+1)	= 8 (3 . 5^2n + k) = 8 . h
Conclusion
Si la propriété est vraie pour une valeur (n) => Elle est toujours vraie pour la valeur suivante (n + 1) Or elle est vérifiée pour n = 1 => Elle est vraie pour tous les nombres suivants

Voir Démonstration par induction

DIVISIBILITÉ PAR 8

de cette forme polynomiale

Théorème

La barre verticale signifie divise

Le chapeau ^ signifie puissance

Démonstration

Pour n = 1
C'est vrai.

2¹ = 2

3² – 1 = 9 – 1 = 8

2¹⁺² = 8

et 8 8

Supposons la formule vraie pour n.

3^{2^n} – 1 = m . 2ⁿ⁺²

L'est-elle pour n + 1?

2ⁿ⁺³ 3^{2^(n+1)} – 1 ?

Calcul

3^{2^(n+1)} – 1

= (3^{2^n} )² – 1

= (m . 2ⁿ⁺² + 1)² – 1

= m² . (2ⁿ⁺²)² + 2 . m . 2ⁿ⁺² + 1 – 1

= m² . (2ⁿ⁺²) (2ⁿ⁺²) + m . 2ⁿ⁺³

= 2ⁿ⁺³ (m² . 2ⁿ⁺¹ + m)

Effectivement nous retrouvons bien la formule avec n remplacé par n+1

2ⁿ⁺³ 3^{2^(n+1)} – 1

Exemples

n	3^2^n - 1	2^n+2 +2	Div
1	8	8	1
2	80	16	5
3	6 560	32	205
4	43 046 720	64	672 605

Suite	Divisibilité de formes polynomiales
Voir	Nombres parfaits  Quand n divise n + 8 ou n + k ? Théorie des nombres – Index Calcul mental – Index
DicoNombre	Nombre 8 Nombre 3 337
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi8.htm