|
|||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 4 Critères de divisibilité et formes polynomiales
divisibles. |
Voir Règles
générales de divisibilité
|
Laquelle de ces
affirmations est fausse? Trouvez la réponse sans effectuer les divisions.
|
|
Critères
en bref Il suffit de
s'intéresser N = …. d u Diz Un nombre est
divisible par 4 si et seulement si:
|
Voir Règles
générales / Divisibilité par 8 avec critères
semblables
|
|
||
|
Un nombre est
divisible par 4 si ses 2 derniers chiffres sont divisibles
par 4. |
Exemples 36 = 4 x 9 1 336 = 4 x 334 … 36 = 4 k Explication 1 336 = 13 x 100 + 36
= 4 x 25 x 13
+ 36 La partie jaune
(les centaines) est toujours divisible par 4; reste à vérifier que le reste
(36) l'est. Ce qui est le cas ici. |
|
|
Démonstration
|
N = 100k + du N = 4 (25k) +
du |
|
|
|
4 (25k) |
|
|
|
du |
|
Voir Expression décimale des nombres
|
|
||
|
Un nombre est
divisible par 4 si 2d + u est divisible par 4. |
Exemples 1 336 => 2
x 3 + 6 = 12 1 344 => 2
x 4 + 4 = 12 |
|
|
Démonstration
|
n = 10d + u |
|
|
|
n = 4 x 2d +
2d + u |
|
|
|
4 x 2d |
|
|
|
2d + u |
|
|
|
||
|
Un nombre est
divisible par 4 si d
pair et u = {0, 4, 8}, ou si d
impair et u = {2,6} |
Exemples 1 336 => 3
impair et 6+2 = 8 divisible. 1 344 => 4
pair et 4 divisible. |
|
|
Démonstration
|
n = 10d + u |
|
|
|
n = 10(2h) + u n = 20h + u Divisible par 4 si u l'est |
|
|
|
n = 10(2h+1) + u n = 20h + 10 + u n = 20h + 8 + 2 + u Divisible par 4 si u + 2 l'est, sans dépasser 10.
|
|
|
DIVISIBILITÉ
par 4 – Pour les matheux |
|
|
|
Un nombre est
divisible par 4 si u étant pair u/2 et d sont de même
parité |
Exemples 1 336 => 3
et 6/2 = 3 sont impairs 1 344 => 4 et
4/2 = 2 sont pairs |
|
|
Démonstration
|
d pair
et u = {0, 4, 8} d impair et u = {2, 6} |
|
|
|
d pair
et u/2 = {0, 2, 4} d impair et u/2 = {1, 3} |
|
|
|
d et u/2 sont de même parité. |
|
|
|
|
|
Tous les nombres divisibles par 4 (N = 4k) sont de la forme : N = (k+1) + (k-1) + (k.1) + (k/1) = 4k impliquant le résultat des quatre opérations. Voir Quatrops |
|
Le plus petit nombre en 3 et 4, divisible
par 3 et 4
|
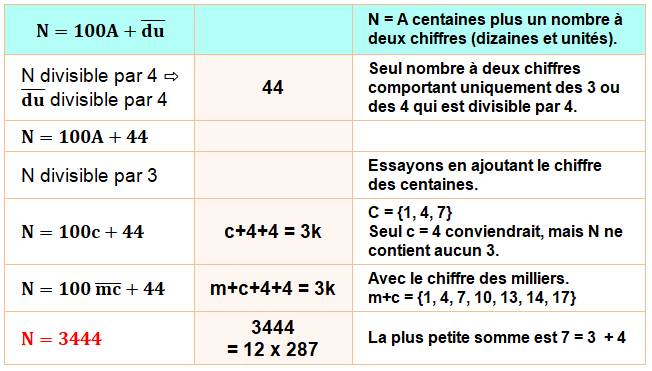
Énigme 1 Quel
le plus petit nombre en 3 et 4 qui est divisible par 3 et 4? Chaque
chiffre (3 et 4) doit être présent au moins une fois. Solution
Les
suivants: 4344, 33444, 34344, 43344 …
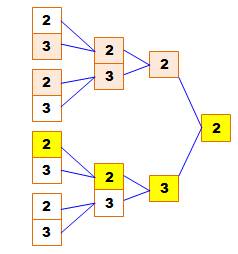
Même question, mais
avec 2 et 3 et N divisible par 2 et 3. Solution N est pair donc le
chiffre des unités est 2 (3 est évidemment impossible). On construit le nombre
en ajoutant les dizaines: aucun n'est divisible par 3; avec les centaines,
non plus. Avec les milliers,
trois chemins montrent des nombres divisibles par, contenant au moins un 2 et
un 3 et que des 2 et des 3: 3222, 2322 et 2232. Et, c'est 2232 est le plus petit.
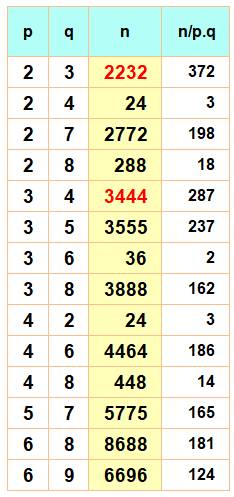
Tous les
nombres les plus petits en p et q divisibles par p et q En rouge, les deux
nombres trouvés ci-dessus. Ne sont montrées que
les valeurs pot p>q, ces deux nombres étant permutables. Les valeurs de p et q
non mentionnées n'offrent aucun résultat. Par exemple, un nombre en 2 et 5 ne
peut a être divisible à la fois par 2 et par 5: il y a conflit au niveau des
unités. Anglais Every digit of a given positive integer is either a 3 or a 4 with each
occurring at least once. The integer is divisible by both 3 and 4. What is
the smallest such integer ? |
|
|
||||
|
Carrés Le carré d'un nombre
pair est divisible par 4. Le carré d'un nombre impair moins 1 est divisible par 4. >>> Théorème
Le reste de la division par 4 d'une somme de carré n'est jamais 3. Démonstration |
||||
|
Formes exprimées en dizaines et unités,
d est un nombre et u un chiffre. |
a = 10d + u b = 10d' + u' |
|||
|
Somme des carrés. |
a² + b² = 100d + 20 du + u² +
100d' + 20d'u' + u'² |
|||
|
Divisibilité par 4 des termes avec facteur
100 et 20. |
(a² + b²) mod 4 = u² + u'² |
|||
|
Seule chose à examiner => |
somme des carrés des unités |
|||
|
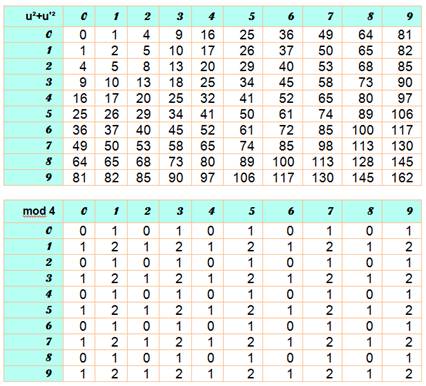
Tableau des possibilités En haut: la somme des carrés des unité. En bas le reste de la division par 4 Aucun reste en 3 |
|
|||
Voir Somme de deux carrés / Modulo
|
|
||
|
|
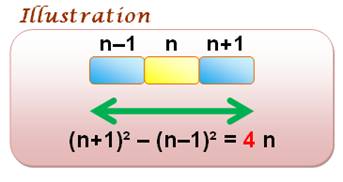
(n + k)² – (n – k)² = 4 k n |
|
|
|
|
|
Voir Divisibilité
par 8 / Écarts entre
carrés
|
|
||
|
Approche Propriété
de divisibilité de la somme et de la différence de deux nombres impairs: Il
semblerait que tous ces nombres soient pairs
et que l'un des deux soit divisible par 4. |
Exemples 5 & 3 => S = 8 et D = 2 7 & 3 => S = 10 et D = 4 9 & 3 => S = 12 et D = 6 11 & 3 => S = 14 et D = 8 |
|
|
Démonstration
|
||
Voir application: Aire du triangle de Pythagore jamais un
carré
|
|
||
|
|
7 – 3 = 4 72 – 32 = 49 – 9 = 40 |
|
|
|
7n – 3n = (7 – 3) (7n-1
+ 7n-2 x 3 +… + 7 x 3n-2 + 3n-1) = 4 k |
|
|
Laquelle de ces
affirmations est fausse?
Le nombre 34 (deux derniers chiffres) n'est pas divisible par 4.
Divisible par 5 car terminé par 5.
Nombre pair et somme des chiffres
divisible par 3; il est divisible par 2 et par 3; il l'est par 6. En prolongeant:
avec 7 et 8, les nombres ne sont pas des multiples. Par contre, avec 9:
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()
Renvois de liens
Divisibilité par 8 de la somme des carrés >>>