NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/01/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
Index général >>> INDEX	Index divisibilité	Nombres en n^k + k^n	Nombres en n^x y
		Nombres en a^n + b^n
		Sommaire de cette page >>> Approche >>> Cas n = 4

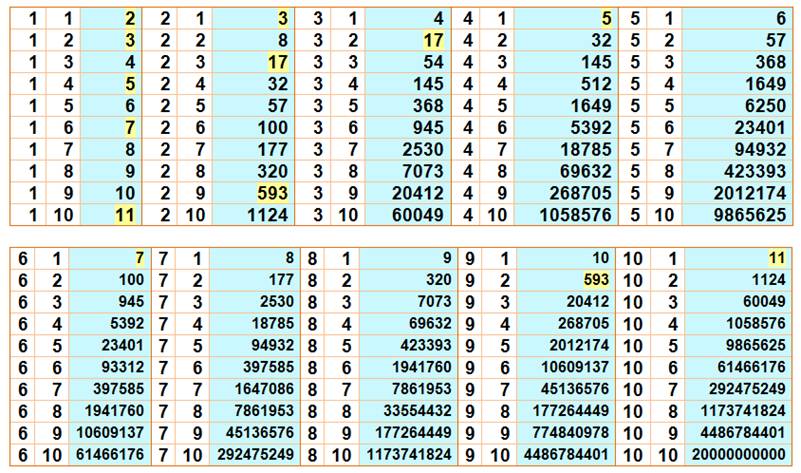
NOMBRES en N^K + K^N

Ces nombres sont rarement premiers.

Dans le cas de k = 4, seul 5 pour n = 1 est premier.

Approche
Table des valeurs de n^k + k^n pour n et k de 1 à 10 Repérage des nombres premiers en jaune Lecture: 1^1 + 1^1 = 2, premier 2^1 + 1^2 = 3, premier 2^5 + 5^2 = 57, composé. Observations Il semble qu'à partir de k = 4, la plupart des nombres n^k + k^n soient composés. En poursuivant les calculs jusqu'à n = 1000, on observerait que pour:

Cas n = 4
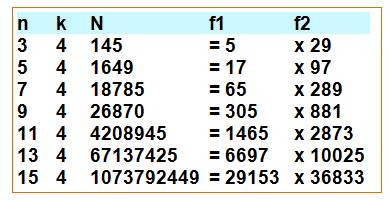
Étude du cas	N = n^4 + 4^n
Si n est pair ü N est pair, donc non premier.	n^4 + 4^n		= (2k)^4 + 4^2k
Si n est impair ü Cherchons une mise en facteur. ü Le premier terme est un carré. ü Le deuxième aussi, finalement.	n^4 + 4^n n^4 4^n		= n^4 + 4^n = (n^2)^2 = (2x2)^n = 2^n.2^n =
Exprimons N ü En somme de deux carrés. ü Essayons de révéler une identité remarquable.	n^4 + 4^n		= (n^2)^2 + (2^n)^2 = (n^2)^2 + (2^n)^2 + 2(n²)(2^n) – 2(n²)(2^n) = (n^2 + 2^n)^2 – 2^n+1 n²
Nous sommes dans le cas où n est impair ü Alors, n+1 est pair. ü Sa moitié est un nombre entier. ü Nouvelle écriture du terme de droite. ü Qui devient un carré.	2^n+1 n²		= 2^(n+1)/2 n . 2^(n+1)/2 n = { 2^(n+1)/2 n }²
Nouvelle expression de N ü Qui conduit à une différence de 2 carrés. ü Et à une factorisation immédiate. ü Donc N est le produit de 2 facteurs; il n'est pas premier. ü À condition de vérifier que ces facteurs sont bien différents de 1.	n^4 + 4^n		= (n^2 + 2^n)^2 – { 2^(n+1)/2 n }² = (n^2 + 2^n – 2^(n+1)/2 n) (n^2 + 2^n + 2^(n+1)/2 n)
Facteurs différents de 1 D'abord, des deux facteurs. ü On se souvient que n > 2. ü Le facteur de gauche est le plus petit, strictement.	(n^2 + 2^n – 2^(n+1)/2 n) < (n^2 + 2^n + 2^(n+1)/2 n)
Étudions ce facteur de gauche ü Pour y révéler une identité remarquable. ü Le premier terme est un carré, il est positif.	F	= n^2 + 2^n – 2^(n+1)/2 n = n^2 – 2.n.2^n/2 + 2^n + 2.n.2^n/2 – 2^(n+1)/2 n = (n² – 2^n)² + 2.n.2^n/2 – 2^(n+1)/2 n
Calculons le second facteur.		2.n.2^n^/2 – 2^(n+1)/2 n
ü Pour quelques valeurs de n. ü Ce facteur est supérieur à 1 pour n > 2	n = 1 2 3 4 5	N = 0,82 2,34 4,90 9,37 16,5
ü Dans tous les cas la somme des deux facteurs est supérieure à 1. ü N est donc bien le produit de 2 facteurs différents de 1.	N n'est pas premier pour n > 1
Quelques valeurs:

Suite	Nombres de Leyland (suite de cette page) Nombres en n^x y
Voir	Calcul mental – Index Divisibilité – Index Divisibilité de 2n 1 Divisibilité des formes Factorielle Fermat Géométrie – Index Nombres répétés Petit théorème de Fermat Théorème de Wilson Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divkxxk.htm