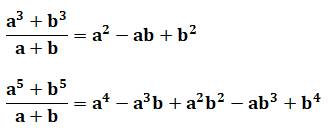|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Divisibilité de an + bn
En bref
|
|||||||||
Voir Identités en a^n
+ b^n et applications
|
|
||
|
Si chaque terme de la somme est divisible par un
nombre, la somme est divisible par ce nombre. Facile! Le reste de la page l'est tout autant Pour un résultat bluffant … |
Exemple 7 Se lit 7 divise 14+28+70 En effet 7 x
2 +
7 x 4 + 7 x 10 = 7
(2 + 4 + 10) =
7 x 16 |
|
|
|
|||
|
Carré |
a2 + b2 |
= (a + b) (a + b) – 2ab NON divisible |
|
|
Cube Divisible par a + b
(cf propriété
ci-dessus) |
a3 + b3 |
= (a2 + b2) (a + b) – a2b
– ab2 = (a2 + b2) (a + b) – ab (a + b) OUI divisible par a + b |
|
|
Puissance n = 4 |
a4 + b4 |
= (a3 + b3) (a + b) – a3b
– ab3 = (a3 + b3) (a + b) – ab (a2+ b2) NON |
|
|
Puissance n = 5 Divisible par a + b |
a5 + b5 |
= (a4 + b4) (a + b) – a4b – ab4 = (a4 + b4) (a + b) – ab (a3 + b3) OUI |
|
|
Etc. |
... |
|
|
|
Puissance n = 2k (paire) NON divisible par
a+b |
a + b |
|
|
|
Puissance n = 2k+1 (impaire) Divisible par a+b |
a + b |
|
|
|
an + bn
est divisible par a +
b pour toutes les puissances n impaires. |
|||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 + 2 pour
tout n imp ou 1n
+ 2n est
divisible par
3 pour tout n
impair ou une puissance de 2 augmentée d'une unité est divisible par 3 pour tout n impair. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 + 3 ou 1n + 3n
est divisible
par
4 pour tout n
impair. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7 + 8 ou 7n + 8n
est divisible
par
15 pour tout n
impair. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
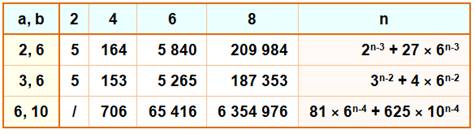
Considérons
la somme des puissances des six premiers nombres. On
peut tout aussi bien l'écrire, en faisant apparaître une somme des chiffres
identique (ici, égale à 7). |
1n
+ 2n + 3n + 4n
+ 5n + 6n (1n + 6n) + (2n + 5n) + (3n + 4n) |
|
|
Or,
nous venons juste de voir que les expressions entre parenthèse sont
divisibles par la somme de leurs nombres. |
7 = 1 + 6 | 1n
+ 6n 7 = 2 + 5 | 2n
+ 5n 7 = 3 + 4 | 3n
+ 4n |
|
|
Les
termes de la somme, pris deux à deux, sont divisibles par 7. La somme est
aussi divisible par 7 (encore une application du rappel de tête). |
(1n + 6n)
+ (2n + 5n) + (3n + 4n) = 7 k + 7 k' + 7k" = 7 (k + k' +
k") |
|
|
Conclusion La somme des puissances des nombres jusqu'à 6 est
divisible par 7 pour toutes les puissances impaires. La
généralisation au-delà du cas particulier de 7 est possible. >>> |
7 | 1n +
2n + 3n + 4n + 5n + 6n pour n = 2k+ 1 |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()