|
|||||||||||||||||||||||||||||
![]()
|
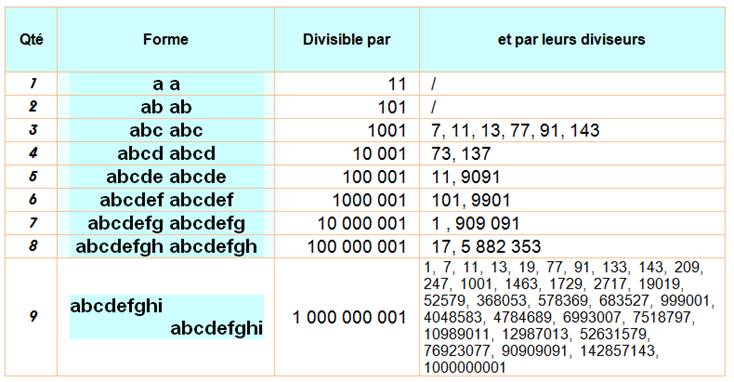
NOMBRES à répétition et leur divisibilité. Occasion de produire des multiplications amusantes et de
concocter des tours de magie. Propriété: Exemple: 123
123 =
1001 Propriété: 1001 =
37 Propriété: 123
123 =
37 |
Voir Divisibilité
/ Divisibilité des nombres
en 9
|
|
||
|
|
1, 101 |
|
|
|
Le produit d'un nombre de deux chiffres par 101 engendre un nombre
répété. 12 12 = 12 x 101 12 x 101 = 12 (100 +
1) = 12 00 +
12 = 12 12 |
|
|
|
Règle générale Le nombre 101 étant premier, aucune possibilité de diviser tous
les nombres tels que 1212 par un nombre autre que 101. Cas particulier Pris individuellement, ces nombres répétés sont
au moins aussi divisible que le nombre source Exemple Facteurs: 1212 = 22 x 3 x 101 |
|
Notes: Les nombres ne sont pas présentés en
bloc de trois pour mieux apprécier les
répétitions.
La barre de surlignement indique qu'il
s'agit d'un nombre et non d'un produit.
|
|
||
|
|
1, 7, 11, 13, 77, 91, 143, 1001 |
|
|
|
123 123 = 123 x 1001 123 x 1001 = 123 (1000
+ 1) = 123 000 +
123 = 123 123 |
|
|
|
Tous les nombres en 123123 =
7 x 17 589 123123 =
11 x 11 193 123123 =
13 x 9 471 123123 =
77 x 1 599 123123 =
91 x 1 353 123123 = 143 x 861 |
|
Configurations permettant des trucs de calcul mental
|
143 x 7 = 1 001 1 667 x 3 = 5 001 142 857 x 7 = 999 999 2 857 143 x 7 = 20 000 001 142 857 143 x 7 = 1 000 000 001 |
|
– Nombres répétés à quatre chiffres |
|
|
|
|
1, 73, 137, 10 001 |
|
|
|
1234 1234 = 1234 x
1001 |
|
|
|
Tous les nombres en 12341234 =
73 x 169 058 12341234 = 137 x 90 082 |
|
|
Cette propriété
est évidente, mais amusante du fait du nombre 365 (jours de l'année). |
365 = 5 x
73 50 005 =
365 x 137 = 5 x 10 001 En plus, si d = 0 ou 5, ces nombres sont divisibles par 365 et par 50
005. 12351235 =
365 x 33 839 12351235 =
50 005 x 247 |
|
|
Avec
101, nous avons vu le principe de la formation d'un nombre répété. Avec
1001, c'est une propriété de divisibilité générale qui se manifeste. Avec
10 001 et ses deux uniques diviseurs (73 et 137), la divisibilité des nombres
répétés à quatre chiffres est difficile à débusquer et, donc, propice à
quelques tours de magie simples. |
|
Je
suis capable de transmission de pensée entre vous deux: Clément et Alexis.
Tu l'inscris sur la calculette et tu
multiplies par 137 sans qu'Alexis te voie. Le nombre N auquel tu as pensé est
bien caché, n'est-ce pas. Alexis va pourtant le deviner.
Il lit les quatre premiers chiffres et
annonce fièrement le nombre à Clément. Les
deux compères sont aussi émerveillés l'un que l'autre! |
Clément
Alexis
|
|
|
|
|
Motif général
|
|
|
|
|
|
A = 12341234 B = 56785678 A + B =
69126912 = 10001 x 6912 A = 12341234 B = 56785678 A + 10 x B =
580198014 = 10001 x 58014 A = 12341234 B = 56785678 2 x A + 10 x B = 592539248 = 10001 x 59248
S = 2345 R = 23452345
R / 365 = 64253 S = 9995 R = 99959995
R / 365 = 273863 |
|
|
|
|
|
Facteurs
Divisibilité
|
|
Voir Nombres 7 / 11 / 13 / 17 / 19 / 73 / 101 / 111 / 137
/ 10
001
|
|
||||
|
111 x
a = aaa |
Facteurs Diviseurs |
3 x 37 1, 3, 37, 111 |
Tous
les nombres en aaa sont
divisibles
par 3, 37 et 111. |
|
|
10101 x
ab = ababab |
Facteurs Diviseurs |
3 x 7 x 13 x 37 1,
3, 7, 13, 21, 37, 39, 91, 111, 10101, 273, 259, 481, 777, 1443, 3367 |
Tous
les nombres en ababab sont
divisibles par 10101 et
par tous ses diviseurs |
|
|
1001001 x
abc = abcabcabc |
Facteurs Diviseurs |
= 3 x 333667 1,
3, 333667, 1001001 |
Tous
les nombres en abcabcabc sont
divisibles par 1001001 et
par ses diviseurs |
|
|
1101011 |
Facteurs Diviseurs |
= 67 x 16 433 1,
67, 16433, 1101011 |
Tous
les nombres en aa0a0aa sont
divisibles par 1101011 et
par ses diviseurs |
|
|
Etc. |
Ce
dernier cas, avec un nombre non symétrique, ne représente pas un grand
intérêt. La propriété n'existe que pour les 9 valeurs de a. |
|||
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()