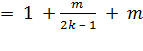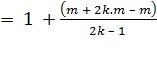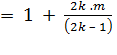|
|||||||||||||||||||||||||||||
![]()
|
|
|
|
Proposition directe: démonstration
par Euclide, il y a 2300 ans. Proposition réciproque:
démonstration par Euler en 1849. Si on connaît un nombre de Mersenne premier 2k – 1, On connaît un nombre parfait
beaucoup plus grand 2k – 1
(2k – 1) |
|
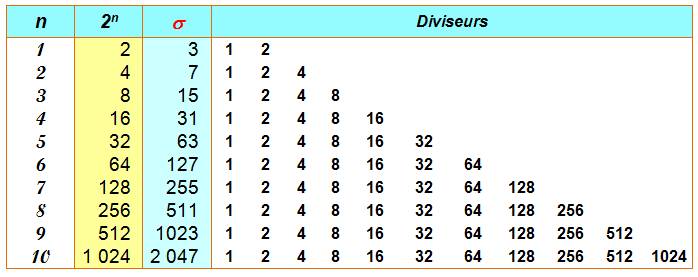
Voir Les plus grands nombres de Mersenne
connus
|
|
||
|
Formule d'Euclide:
Théorème Si (2k – 1) est premier, alors N = 2k – 1
(2k – 1) est parfait. Conclusions |
||
|
2k – 1 |
|
|
|
M = 2k – 1 |
|
|
|
M premier |
|
|
|
M composé |
|
|
|
|
|||
|
Ce qu'il faut
démontrer (CQFD)
Principe |
|||
|
N
= |
2k-1 |
. p (premier) |
|
|
|
=
ceux de 2k-1 |
+
les précédents multipliés par p |
|
|
|
|
Constater
ce fait |
|
|
Démonstration |
|||
|
Posons le problème |
|
|
|
|
|
p |
=
2k – 1 |
|
|
|
n |
= 2k – 1 . p |
|
|
|
|
= 2n |
|
|
|
2n |
= 2
. 2k-1 .
p = 2k
. p |
|
|
Les diviseurs de n
sont: |
|
|
|
|
|
2k – 1 |
1,
2, 2², …, 2k-1 |
|
|
|
|
1,
p |
|
|
|
|
p, 2.p, …, 2k-1 .p |
|
|
|
Diviseurs de n
|
1, 2, 2², …, 2k-1 , p, 2.p, …, 2k-1 .p |
|
|
Somme des diviseurs |
|
|
|
|
|
|
= 1 + 2 + 2² + …+ 2k-1 + p + 2.p + … + 2k-1 .p |
|
|
|
|
= (1 + 2 + 2² + …+ 2k-1) (1 + p) |
|
|
|
|
=
|
|
|
Évaluons les termes |
|
|
|
|
est
égale à la puissance supérieure moins1 |
|
=
(1 + 2 + 2² + …+ 2k-1) =
2k – 1 + 1 – 1 =
2k – 1 |
|
|
|
|
= 1 + p = 1 + 2k –
1 =
2k |
|
|
Bilan |
|
|
|
|
|
|
= (2k – 1) . 2k
= 2
. 2k – 1 (2k – 1) |
|
|
Et CQFD |
|
= 2 . n |
|
|
|
|||
|
Ce qu'il faut
démontrer (CQFD)
Principe |
|||
|
1.
Tout entier naturel est de la forme:
|
n
= 2k – 1 .
m |
||
|
2.
On cherche à exprimer la somme des diviseurs: |
|
||
|
3.
Que l'on compare à celle connue, car n
est parfait. |
|
||
|
4.
On a deux évaluations de la somme; l'égalité va être
exploitée. |
|||
|
5.
On connait trois diviseurs. |
1,
M et m |
||
|
6.
Un raisonnement par l'absurde nous amène à constater que
M = 1: il doublonne, il faut l'éliminer. |
1,
m |
||
|
7.
et à conserver un nombre premier de la forme cherchée |
m
= (2k – 1) |
||
|
|
|||
|
Posons le problème |
|
|
|
|
avec
et,
n étant pair (hypothèse) |
n m k |
=
2k – 1 .
m Impair
|
|
|
Diviseurs de n |
|
|
|
|
|
=> => |
2,
2a, 2b, … 3,
5, 7 ou autres mais
jamais 2 |
|
|
Somme des diviseurs
de n |
|
|
|
|
|
n
|
=
2k – 1 .
m =
s(2k – 1) . s(m) |
|
|
|
|
=
(2k – 1) |
|
|
|
|
=
(2k – 1) . s(m) |
|
|
Somme des diviseurs du
nombre parfait n |
|
|
|
|
|
|
=
2 . n |
|
|
|
|
=
2 . 2k – 1 . m =
2k . m |
|
|
|
2k . m |
(2k - 1) . s(m) |
|
|
Divisibilité |
|
|
|
|
|
|
= 2k .
m / (2k - 1) |
|
|
Or,
les termes en puissance de 2 sont premiers entre eux |
(2k – 1)
|
ne
divise pas 2k |
|
|
Donc,
c'est m qui est divisible |
m / (2k
– 1) |
=
M entier |
|
|
Voilà
un nouveau diviseur |
de m |
donc
de n |
|
|
On connaît des
diviseurs de m |
|
|
|
|
|
|
1,
M et m |
|
|
|
s |
=
1 + M + m |
|
|
|
s |
= 1 + s |
|
|
Contradiction et
conséquences |
|
|
|
|
|
|
1,
M et m |
|
|
Il
y en a deux qui sont incontournables: |
|
1 & m qui est premier |
|
|
Seul
le troisième permet de lever la contradiction si on le pose égal à 1 M
= 1 et 1 sont des doublons Un
seul des deux est conservé |
M |
=
1 |
|
|
On
en déduit la valeur de m |
m |
= (2k – 1) |
|
|
Or,
hypothèse: |
n |
=
2k – 1 .
m |
|
|
Conclusion |
|
|
|
|
|
n |
= 2k – 1
. (2k
– 1)
(2k
– 1) premier |
|
|
|
|
|
Observation
Théorème
Exemple pour n = 3: |
|
Voir Puissance
de 2 / Multipuissances
|
|
|||
|
|
n = 2a . u |
u impair |
|
|
S'il
est impair : |
n = 20 . u |
a = 0 |
|
|
S'il
est pair, on toujours sortir ce qu'il a de pair. |
n = 2a . u |
a |
|
|
|
|||
|
|
n |
=
2k – 1 (2k – 1) =
2k – 1 . c |
|
|
Les diviseurs de n
sont, au moins |
|
|
|
|
|
2k – 1 => |
1,
2, 2², …, 2k-1 |
|
|
|
=> |
c, 2.c, …, 2k-1 .c |
|
|
|
|
|
|
|
|
s(n) |
= 2 . n |
|
|
Mais n est composé |
|
|
|
|
|
=> |
au
moins un d |
|
|
|
s(n) |
³ 2 . n + d |
|
|
|
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Parfdemo.htm |
![]()