|
||||||||||||||||||||||||||||
![]()
|
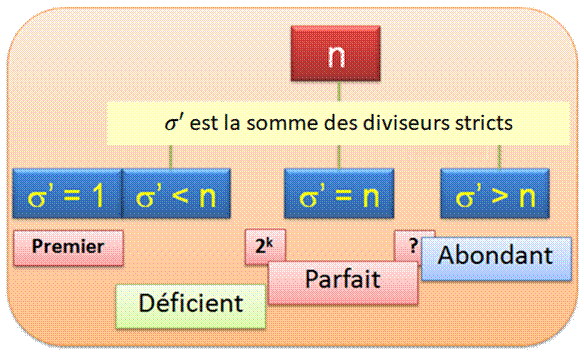
Nombres ABONDANTS, PARFAITS & DÉFICIENTS On considère les diviseurs d'un nombre, sauf le nombre lui-même
(diviseurs propres ou diviseurs stricts). On effectue leur somme (s') ; on compare le nombre
initial à cette somme … Le nombre n est parfait
en cas d'égalité. À un près, le nombre est presque-parfait.
Les nombres presque-parfaits de déficience 1 sont
les puissances de 2; on ne connait pas de presque-parfait avec
abondance de 1. Voir rubrique débutants pour
une introduction en douceur >>> |
Anglais: Abundant, perfect and deficient
numbers
|
|
|
|
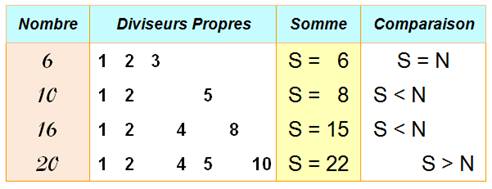
Observations Le chiffre 6 est
divisible par 1, par 2 et par 3. Il est curieux car la somme de ses diviseurs
est justement 6. Notez que l'on prend les
diviseurs, avec le 1 et sans le 6. Ce sont les diviseurs propres Le nombre 10 donne la
somme de 8
qui est inférieur à 10. Le nombre 20 donne la
somme de 22 qui est supérieur à 20. Trois possibilités
Pour
en savoir plus C'est Nicomachus
en 100 après J.-C. dans son livre Introductio Arithmetica qui
introduisit ces noms. |
|
Voir Définitions
|
Déficients
Abondants
171 078 831 171 078 832
Diviseurs
de 90 : {1, 2, 3, 5, 6, 9, 10, 15,
18, 30, 45, 90}. En rouge, les
déficients.
Diviseurs
de 20: {1, 2, 4, 5, 10, 20}. Nombre = somme
des diviseurs abondants. Diviseurs
de 24: {1, 2, 3, 4, 6, 8, 12, 24}. Nombre pas égal à la somme des diviseurs
abondants. |
|
|
|
||
|
|
Programme de recherche des nombres égaux à la somme de leurs
diviseurs déficients Appel
des logiciels de théorie des nombres. Lancement
de la boucle d'analyse des nombre n de 2 à 10000. Si
la somme des diviseurs (sigma) n'est pas égale à 2n, on poursuit en évitant
les nombres parfaits. La
liste des diviseurs est dans A et la somme des diviseurs que nous cherchons (S) est initialisée à 0. Boucle
d'analyse des diviseurs de 1 à quantité de diviseurs (nops). Si
le diviseur est déficient, alors on ajoute sa valeur à S. Fin
de condition (fi) et fin de boucle (od). Si
la somme trouvée S est gale au nombre n, alors le faire savoir en
l'imprimant. En
bleu, résultat de l'exécution du programme. Seul 90 ressort pour n jusqu'à 10
000 (et c'est vrai jusqu'à 1 milliard). |
|
Voir Programmation – Index
|
|
||
|
Nombres
tels que:
Ce sont
les nombres abondants record: la somme de ses diviseurs est supérieure à
celle de tous les autres nombres plus petits. |
1, 2, 3, 4, 6, 8, 10, 12, 16, 18, 20, 24, 30, 36,
42, 48, 60, 72, 84, 90, 96, 108, 120, 144, 168, 180, 210, 216, 240, 288, 300,
336, 360, 420, 480, 504, 540, 600, 630, 660, 720, 840, 960, 1008, 1080, 1200,
1260, 1440, 1560, 1620, 1680, 1800, 1920, 1980, 2100, 2160, 2340, 2400, 2520,
2880, 3024, 3120, 3240, 3360, 3600, 3780, 3960, 4200, 4320, 4620, 4680, 5040,
5760, 5880, 6120, 6240, 6300, 6720, 7200, 7560, 7920, 8400, 8820, 9240, … |
|
|
|
|||||
|
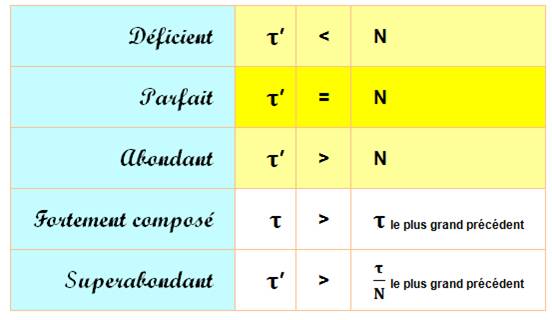
Définition Selon définition de Ramanujan , en partant de 1, suite des
nombres qui établissent un nouveau record en quantité de diviseurs. Plus
précisément, n est fortement composé si:
Exemples
Premiers nombres fortement
composés 1,
2, 4, 6, 12, 24, 36, 48, 60, 120, 180 >>> Ramanujan Le plus grand trouvé par Ramanujan: 6 746 328 388 800 = 26 x 34 x 52 x 72
x 11 x 13 x 17 x 19 x 23 Il prouve pour tout nombre hautement composé, les
exposants des facteurs premiers successifs vont en décroissant. Chaque
exposant est plus grand ou égal au suivant. Le dernier exposant est toujours égal à 1, sauf
pour 4 et 36. Il en existe une infinité. |
|||||
Anglais:
Highly
composite numbers
Suite Nombres hautement composés
Voir Unitairement
parfait / Types de nombres selon leurs
diviseurs / Table
de diviseurs
|
|
|
|
|
|
Anglais:
Superabondant
numbers
|
|
|
|
Exemple 70
= 2 x 5 x 7 Somme
des diviseurs propres: 1 + 2 + 5 + 7 + 10 + 14 + 35 = 74 => abondant; Diviseurs
2, 5 et 7 sont premiers => déficients; Diviseur
10 = 2 x 5 et somme des diviseurs: 1 +
2 + 5 = 8 => déficient; Diviseur
35 = 5 x 7 et somme des diviseurs: 1 + 5 + 7 = 13 => déficient. 70
est un nombre abondant primitif. Liste 20,
70, 88, 104, 272, 304, 368, 464, 550, 572, 650, 748, 836, 945, 1184, 1312, 1376, 1430, 1504, 1575, 1696, 1870,
1888, 1952, 2002, 2090, 2205, 2210, 2470, 2530, 2584, 2990, 3128, 3190, 3230,
3410, 3465, 3496, 3770, 3944, 4030, 4070, 4095, 4216, 4288 … 945
est le plus petit impair. Voir Nombre semi-parfaits
primitifs |
|
Anglais:
Primitive
abondant numbers
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Abondant.htm |
![]()