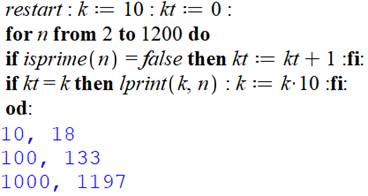|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
Définition Entiers
naturels non premiers. Anglais: Composite numbers,
neither prime, nor equal to 1. Exemples 4 = 1 x 2 x 2 Diviseurs: 1, 2, 4 35 = 1 x 5 x 7 1, 5, 7, 35 111 = 1 x 3 x 37 1, 3, 37, 111 Théorème fondamental de l'arithmétique Tout
nombre entier naturel est décomposable de
façon unique en produit de ses diviseurs premiers, sans tenir compte des
permutations. Voir ce théorème |
|
|
|
|||
|
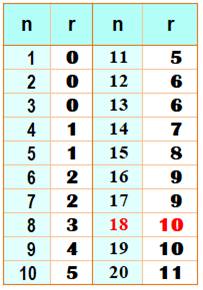
Identification du 10e
nombre composé
Il y a 10 nombres composés jusqu'à 18 + 7 nombres premiers + le nombre 1, qui n'est ni premier ni composé. |
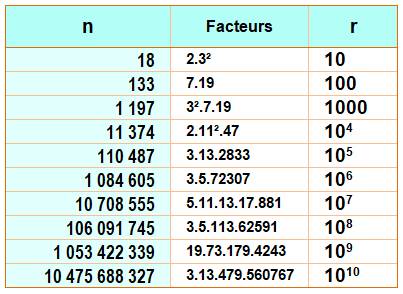
Nombres composés de rang k = 10r
La quantité de nombres premiers pour arriver à 10r nombres
composés est égale à n – r, soit les chiffres significatifs après le 1
initial de n Ex: il y 84 605 premiers pour arriver au composé de rang 106 |
||
|
Programmation du comptage (Maple)
|
Programme simple de comptage des nombres composés Initialisation et préparation de compteurs. Boucle d'analyse des nombres n de 1 à 1200. Si le nombre n n'est pas premier, le compteur kt est incrémenté. Chaque fois que le compteur atteint une puissance de 10, demande
d'impression. |
||
Voir Programmation – Index
|
|
|
|
Question
Réponse
|
|
|
|
||
|
Définition Nombre compose situé à égale distance de deux
nombres premiers successifs. Records Les nombres interpremiers sont aussi nombreux que
les nombres premiers, en quantité infinie. Cas intéressant: quels sont les nombres
interpremiers appartenant à un espace entre premiers de plus en plus grand. La distance est indiquée dans la colonne de
droite du tableau et marquée en rouge pour les records. Le tableau du bas montre les records jusqu'à un
million |
Nombre interpremiers jusqu'à 100
|
|
|
|
||
|
Nombre composé somme de tous les nombres
premiers compris entre son plus petit facteur
et son plus grand. |
Exemple: 10 = 2 x 5
= 2 + 3 + 5 Liste: 10, 39, 155, 371, |
|
|
|
||
|
La majorité des nombres
composés sont somme de deux nombres premiers Rappel: conjecture de
Goldbach: tout nombre entier > 5 est la somme de trois premiers. |
Nombres composés NON somme de deux
premiers jusqu'à 500: Ce sont les nombres impairs n tels que n – 2 n'est pas premier: 27,
35, 51, 57, 65, 77, 87, 93, 95, 117, 119, 121, 123, 125, 135, 143, 145, 147,
155, 161, 171, 177, 185, 187, 189, 203, 205, 207, 209, 215, 217, 219, 221,
237, 245, 247, 249, 255, 261, 267, 275, 287, 289, 291, 297, 299, 301, 303,
305, 321, 323, 325, 327, 329, 335, 341, 343, 345, 357, 363, 365, 371, 377,
387, 393, 395, 405, 407, 413, 415, 417, 425, 427, 429, 437, 447, 453, 455,
471, 473, 475, 477, 483, 485, 495, 497 … |
|
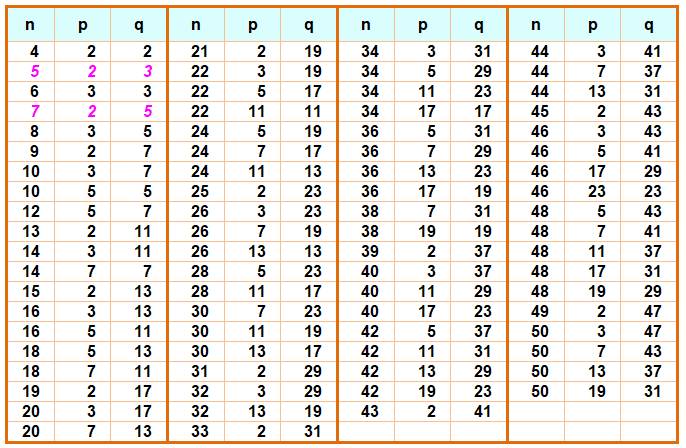
Nombres
composés somme de deux premiers jusqu'à 50
Les nombres premiers
(sauf 5 et 7) ne sont pas signalés.
Notez que les nombres
impairs qu'avec 2 pour l'un des premiers.
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
