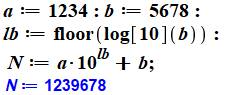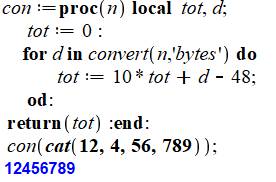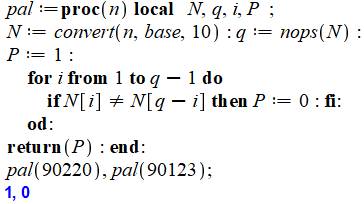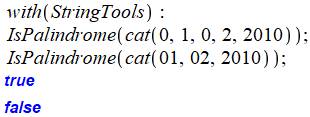|
||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Dates
palindromes actuelles
![]()
|
DATES PALINDROMES ETADATE On peut s'intéresser à l'année: 2002 ou à la date complète: 10 02 2002 et même avec l'heure: 20h 02 le 20 02
2002 Les
dates peuvent prendre plusieurs formes:
|
Voir Dates curieuses, chanceuses …
|
|
||
|
Cette date constitue un palindrome en l'écrivant
à l'européenne comme à l'américaine. Rare. Certains cherchons le raffinement avec le 2
février 2020 à 02 h 02 minutes 20 secondes et 20 centièmes: 02
02 2020 02 02 20 20 |
|
|
|
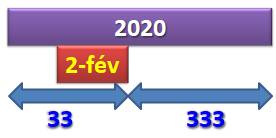
Extraordinaire, du fait que 2020 est bissextile:
le 2 février est le 33e jour de l'année et il reste 333 jours pour
finir l'année. |
|
|
Voir
2020 – Bonne année avec humour / Nombre 2020
– Curiosités et jeux
|
|
||
|
Année palindrome
= produit de palindromes |
||
|
1111 = 11 x 101 1331 = 11 x 11 x 11 1441 = 11 x 131 1661 = 11 x 151 1881 = 11 x 171 1991 = 11 x 181 |
2112 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x
11 2222 = 2 x 11 x 101 2662 = 2 x 11 x 11 x 11 2772 = 2 x 2 x 3 x 3 x 7 x 11 2882 = 2 x 11 x 131 |
|
Dates curieuses (moins de 8 chiffres)
|
|
|
||
|
10 02
2001 |
|
|
|
29 11 1192 |
|
|
|
|
|||
|
20 h 02 |
20 02
2002 |
|
|
|
10 h 01 11 h 11 |
10 01 1001 11 11 1111 |
|
|
|
21 h 12 |
21 12 2112 |
|
|
|
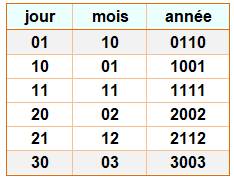
S’en convaincre : L’analyse sur les jours (1 à 31) et
les mois (1 à 12) donnent six possibilités. La première nécessite des 0 en tête
pour faire : 0110 0110 0110 ; sans ces 0 on a
la répétition : 110 110 110. La dernière est valide pour la date,
l’année, mais pas pour l’heure : 30 h et 3 min n’existe pas. |
|
||
|
|
|||
|
20 h 02 20 h 02 20 h 02 20 h 02 20 h 02 |
10 01 2002 20 02 2002 01 10 2002 11 11 2002 21 12 2002 |
|
|
|
|
|||
|
11 11 2002 12 11 2002 13 11 2002 14 11 2002 15 11 2002 21 11 2002 22 11 2002 23 11 2002 24 11 2002 25 11 2002 11 12 2002 12 12 2002 13 12 2002 14 12 2002 15 12 2002 21 12 2002 22 12 2002 23 12 2002 24 12 2002 25 12 2002 31 12 2002 |
11 h 11 11 h 21 11 h 31 11 h 41 11 h 51 11 h 12 11 h 22 11 h 32 11 h 42 11 h 52 21 h 11 21 h 21 21 h 31 21 h 41 21 h 51 21 h 12 21 h 22 21 h 32 21 h 42 21 h 52 21 h 13 |
|
|
![]()
|
|
||
|
Lecture du tableau Ce
tableau liste toutes les dates palindromes de l'année 2000 à l'année 2050. Pour
chacune, quatre colonnes:
Pour la date,
trois formats:
Les
doublons sont conservés et le nombre en bleu indique:
|
Commentaires Le tableau comporte cinq dates en 29 février dont
les dates sont divisibles par 4 (années: 92, 292, 1292, 2292 et 2092,
soulignées en marron). Elles sont bissextiles
et comportent bien un 29 février. Les jours du 5 octobre au 14 octobre 1582
n'existent pas. Aucune date palindrome dans cette période. Certaines anomalies
du calendrier ne sont pas prises en compte ici. Par exemple: l'année 46 comporte 455 jours et l'année 1582 en
compte 355. Sans compter d'autres années modifiées. Décompte Il y a 2 363 dates palindromes des années 1 à 3
000 sur un peu plus d'un million de dates effectives. Les seules années de 1 à 10 comptent 135 dates palindromes
pour 2 seulement entre 2000 et 2010 et 29 entre 2000 et 2100. |
|
|
Dates de 200 à 2050: JJ MM puis Année |
Année
puis MM JJ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
01
01 pour le 1er
janvier |
1
ou 01 pour janvier |
01
01 pour le 1er
janvier |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Grands sauts de huit siècles !
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Suite pour les dates de 1 à 3000
Voir 2011 et
palindromes / 2020 / 2021
/ Brève
de maths 552
Merci à Guillaume Perret
pour ses suggestions
|
|
|||
|
Un
programme testant si une date est palindrome serait simple à réaliser. Nous
voulons ici, établir la liste des dates palindromes dans une plage du
calendrier Le
programme est un peu long, mais d'un abord simple. Il y cependant quelques
obstacles à vaincre comme: obtenir un seul nombre à partir d'une date ou
encore ne se consacrer qu'aux dates valides. |
|||
|
|
Procédure NOMBRES CONCATÉNÉS But Concaténer plusieurs nombres de taille quelconque
et obtenir un nouveau nombre. Ce sera utile pour transformer le 1er
février 2021, en 122021 ou 01022021 ou même 20120101 Solution par puissances de 10 Calculer la taille du nombre et utiliser les
puissances de 10. C'est possible. Une autre méthode consiste à concaténer et à
convertir la chaine de caractères en nombre. Ici, la concaténation est convertie en bytes lesquels sont en fait les chiffres
augmentés de 48 >>> |
||
|
|
Solution par concaténation Procédure con
qui reçoit une chaine (string) de nombres
concaténés. La chaine est convertie en bytes et chacun diminué de 48 va être utilisé pour
construire le nombre (tot). Essais avec quatre nombre concaténés (cat) dont la sortie sera la chaine de caractères
`12456789`; elle-même traitée par la procédure con. |
||
|
|
Procédure PALINDROME But Tester si un nombre est palindrome,
sachant que le chiffre d'en-tête (ici 9) est non-significatif. Solution Conversion du nombre concaténé en liste de
chiffres (convert) qui les délivre à
l'envers. Boucle de test sur les chiffres i et q-i (et non
i et q+1-i du fait de l'inversion). Le nombre est déclaré palindrome a priori
(P = 1) et passe à 0 s'il existe la moindre différence entre chiffres. |
||
|
|
Procédure PALINDROME (direct) On aurait pu utiliser les instructions de
traitement de chaines de caractères de Maple. Attention: les "0" de début de nombres
sont automatiquement éliminés. Ce qui explique que le programme proposé
concatène les nombres avec un
"9" muet en tête du nombre. |
||
|
|
Programme PRINCIPAL But Établir la liste des dates valides qui sont des
palindromes. Le format est le 01 02 2021 (avec des "0" de complément). Le programme pourra facilement s'adapter à
différents formats de dates. Solution bmin et bmax
précisent la plage de calculs. kt compte
la quantité de dates palindromes La liste M répertorie la quantité de jours dans
chaque mois. Suivent quatre modules de trois boucles:
La concaténation est adaptée aux nombres traités
par chaque module:
Résultat du traitement
|
||
|
Listing du code à copier-coller
dans Maple Allez dans Format
/ Convertir / Math 2D pour disposer d'un programme mis en forme
automatiquement. |
restart: pal := proc (n) local N, q, i, P; N :=
convert(n, base, 10); q := nops(N); P := 1; for i to q-1 do if N[i] <>
N[q-i] then P := 0 end if end do; return P end proc; con := proc (n) local
tot, d; tot := 0; for d in convert(n, 'bytes') do tot := 10*tot+d-48 end do;
return tot end proc; bmin := 2000; bmax := 2050; kt := 0; M := [31, 29, 31,
30, 31, 30, 31, 31, 30, 31, 30, 31]; for a from bmin to bmax do for m to 9 do
for j to 9 do d := cat(9, 0, j, 0, m, a); date := con(d); di := cat(0, j, 0,
m, a); if pal(date) = 1 then lprint(j, m, a, di); kt := kt+1 end if end do
end do end do; for a from bmin to bmax do for m from 10 to 12 do for j to 9
do d := cat(9, 0, j, m, a); date := con(d); di := cat(0, j, m, a); if
pal(date) = 1 then lprint(j, m, a, di); kt := kt+1 end if end do end do end
do; for a from bmin to bmax do for m to 9 do for j from 10 to M[m] do d :=
cat(9, j, 0, m, a); date := con(d); di := cat(j, 0, m, a); if pal(date) = 1
then lprint(j, m, a, di); kt := kt+1 end if end do end do end do; for a from
bmin to bmax do for m from 10 to 12 do for j from 10 to M[m] do d := cat(9,
j, m, a); date := con(d); di := cat(j, m, a); if pal(date) = 1 then lprint(j,
m, a, di); kt := kt+1 end if end do end do end do: kt; |
||
Voir Programmation – Index
![]()
![]()
|
|
|
|
Voir |
|
|
Sites |
Voir site
de Patrick De Geest
|
|
Cette page |
![]()