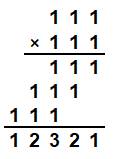|
||||||||||||||||||||||||||||||||||||
![]()
|
PALINDROMES en 11, 101, 111 … Leurs premières puissances restent palindromes. |
Voir Palindromes
carrés à racines particulières
|
Racine des nombres "en
toit" (En référence à la symétrie par rapport au
chiffre central) Note: la racine carrée de 123456789 est
11111,111060… Amusements
sur calculette proposés par Paul
Villemin Voir Brève
de maths n° 583 |
n |
|
Exemple de multiplication posée
|
|
121 |
11 |
||
|
12321 |
111 |
||
|
1234321 |
1 111 |
||
|
123454321 |
11 111 |
||
|
12345654321 |
111 111 |
||
|
1234567654321 |
1 111
111 |
||
|
123456787654321 |
11 111
111 |
||
|
12345678987654321 |
111
111 111 |
Voir Racine carrée des
repdigits
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
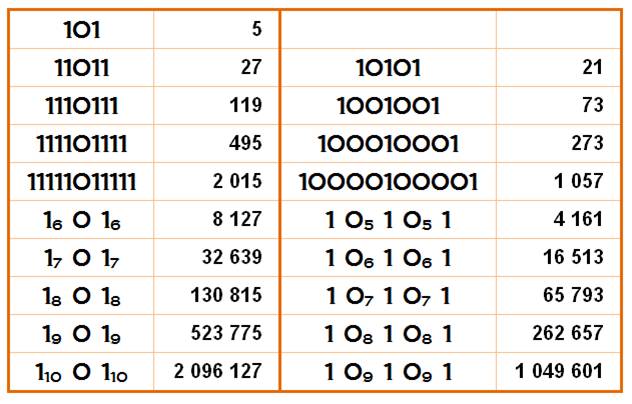
Dans
les cellules bleues:
Dans
les cellules blanches:
Exemple: 113 = 1331, palindrome >>>
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Qté
Repdigit
Son carré 2
11
121 3
111
12321 4
1111
1234321 5
11111
123454321 6
111111
12345654321 7
1111111
1234567654321 8
11111111
123456787654321 9
111111111 12345678987654321 10
1111111111
1234567900987654321 11
11111111111
123456790120987654321
|
|
Voir Brève
428
|
|
|
|
L'année 2015
présente cette particularité d'être un palindrome binaire |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()