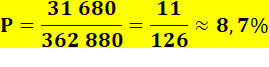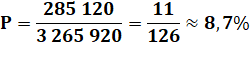|
Édition du: 26/11/2021 |
|
INDEX |
PANNUMÉRIQUES |
||
![]()
|
NOMBRES PANNUMÉRIQUES divisibles par 11 Combien de
nombres pannumériques (nombres formés avec tous les chiffres de 1 à 9) sont divisibles
par 11 ? Ils sont 31
680 et représentent 8,7% des nombres pannumériques. Dénombrement
détaillé. |
||
|
|
Sommaire de cette page >>> En bref >>> Divisibilité par 11 et pannumériques >>> Deux ensembles de chiffres >>> Dénombrement >>> Quelques pannumériques divisibles par 11 |
Débutants Glossaire |
|
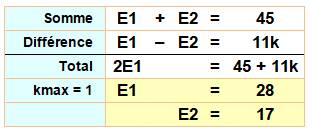
Un nombre pannumérique est composé des neuf
chiffres dont la somme est 45. Pour être divisible par 11, la somme sur
quatre chiffres diminuée de la somme sur cinq chiffres doit être un multiple
de 11, ce qui conduit à 28 – 17 = 11. Il existe 11 possibilités de réaliser
ces sommes avec 4! façons de permuter les quatre chiffres et 5! pour les cinq
chiffres. Bilan, il existe 11 x (4! x 5!) = 31 680 nombres pannumériques
divisibles par 11. |
Voir Brève
805
|
Rappel du critère de divisibilité
par 11 La différence entre la somme des chiffres de rang
impair et ceux de rang pair est divisible par 11. |
Exemple avec le pannumérique
123456789
25 – 20 = 5
=> ce nombre n'est pas divisible par 5. |
||
|
Pannumériques divisibles par 11 La somme des chiffres des chiffres de 1 à 9 est:
45. Pour être divisible par 11, il faut deux
ensembles de chiffres totalisant 55 et dont la différence des sommes est un
multiple de 11. Pour former un nombre de neuf chiffres, il faut
cinq chiffres de rang impair et quatre de rang pair. |
Deux ensembles de chiffres l'un de quatre
chiffres et l'autre de cinq. L'un totalisant 28 et l'autre 17. |
||
|
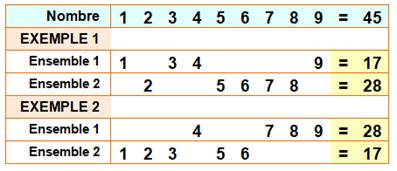
Exemples Un exemple avec ensembles de quatre nombres.
totalisant 17 et cinq nombre pour 28; et inversement. NB. les
nombres 1, 3, 4, et 9 seront en position paire et les autres en position
impaire. Ce qui conduit au nombre: 215364798, par exemple. |
|
||
|
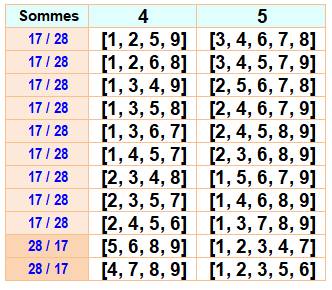
Les 11 sommes 17 + 28 = 45 Il existe neuf ensembles de quatre chiffres qui
ont une somme égale à 17, les autres chiffres étant alors fixés. Il existe neuf ensembles de cinq chiffres qui ont
une somme égale à 17, les autres chiffres étant alors fixés. Exemple avec la dernière ligne 142738596 = 11 x 12976236 |
|
||
|
Explications Choix des chiffres de rang
impair (rang: 1, 3, 5, 7, 9). Un fois un choix fait, il y a 120 façons de les
mélanger (permutations).
Même chose pour les quatre chiffres restants avec
24 autres permutations. |
|
|
|
On peut choisir les chiffres de l'ensemble impair
(2 cas), alors les chiffres de rang pair sont fixés; On peut choisir les chiffres de l'ensemble pair
(9 cas), alors les chiffres de rang impair sont fixés; Il y a donc 11 (2 + 9) façons de choisir ces
ensembles de chiffres (cf. le tableau ci-dessus). Une fois ce choix
effectué (1 parmi 11), les chiffres peuvent être permutés. Soit la quantité de nombres pannumériques
divisibles par 11: 11 x (24 x 120) =
31 680. Or la quantité de permutations des neuf chiffres
est: 9! = 362 880. En choisissant les chiffres au hasard la
probabilité de tirer
Pannumériques complets (avec le
"0")
|
||
Quelques pannumériques divisibles par 11 et
leur quotient
|
123475869,
11225079 123475968,
11225088 123476859,
11225169 123476958,
11225178 123485769,
11225979 123485967,
11225997 123486759,
11226069 123486957,
11226087 123495768,
11226888 |
987632514,
89784774 987641325,
89785575 987641523,
89785593 987642315,
89785665 987642513,
89785683 987651324,
89786484 987651423,
89786493 987652314,
89786574 987652413,
89786583 |
|
Tous ces nombres multipliés par 10, c'est-à-dire avec un "0"
ajouté en queue, sont également divisibles par 11. |
Le plus petit: 123475869 Le plus grand: 987652413 Avec tous les chiffres y compris le "0": Le plus petit: 1024375869 Le plus grand: 9876524130 |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |