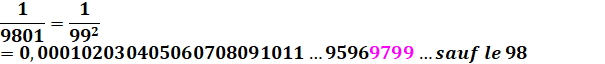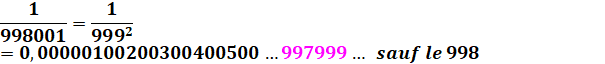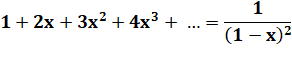NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2023 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Nombres
Débutants Nombres	Particuliers				Glossaire Nombres
INDEX Nombres Taxonomie des nombres	12 345 679	142 857	123 456 789	Autres
	Sommaire de cette page >>> Propriétés mathématiques >>> Nombre phénix de Lewis Carroll >>> Motif amusant >>> Conjecture >>> Fractions avec 81 >>> Fractions qui engendrent presque tous les entiers

Nombre de Lewis CARROLL

12345679 _{sans 8}

Où il est aussi question des nombres spéciaux: 9801 ou 998001

Fraction qui produit tous les nombres de 0 à 999 (sauf 998)

Suite >>>

Propriétés MATHÉMATIQUES

Facteurs	12 345 679 = 37 x 333 667
Diviseurs	1, 37, 333 667, 12 345 679
Quantité	4
Somme	12 679 384
S - N	333 705

impair

composé

Carroll

Facteurs	123 456 790 = 2 x 5 x 37 x 333 667
Diviseurs	1, 2, 5, 10, 37, 74, 185, 370, 333667, 667334, 1668335, 3336670, 12345679, 24691358, 61728395, 123456790
Quantité	16
Somme	228 228 912
S - N	104 772 122

pair

composé

Voir

Nom des nombres

Nombres géométr.

Nombre phénix de Lewis Carroll

12345679: Nombre presque pannumérique, le 8 est absent. Fraction Multiplications pannumériques 12345679 x 1 = 12345679 Pannumérique sans 8 2 = 24691358 Pannumérique sans 7 3 = 37037037 Répétition de 37 4 = 49382716 Pannumérique sans 5 5 = 61728395 Pannumérique sans 4 6 = 74074074 Répétition de 2 x 37 = 74 7 = 86419753 Pannumérique sans 2 8 = 98765432 Pannumérique sans 1, dans l'ordre inverse 9 = 111111111 Répétition de 3 x 37 = 111 Ce nombre redonne tous les chiffres de 1 à 9 lorsqu'il est multiplié par un nombre à un chiffre, sauf pour les multiples de 3, (lui-même étant divisible par 3: 123 456 679 = 13 717 421 x 9). Voir Division par 9 des repunits

Multiplications repdigit

12 345 679 x 9 x 1 = 111 111 111

12 345 679 x 9 x 2 = 222 222 222

12 345 679 x 9 x 3 = 333 333 333

12 345 679 x 9 x 4 = 444 444 444

12 345 679 x 9 x 5 = 555 555 555

Etc.

La suite:

1, 111111111

2, 222222222

3, 333333333

4, 444444444

5, 555555555

6, 666666666

7, 777777777

8, 888888888

9, 999999999

10, 1111111110

11, 1222222221

12, 1333333332

13, 1444444443

14, 1555555554

15, 1666666665

16, 1777777776

17, 1888888887

18, 1999999998

19, 2111111109

20, 2222222220

Repunit

12 345 679 = 111 111 111 x 1, 111 …

111111111 x 1,111 = 123444444,3

111111111 x 1,1111 = 123455555,4

111111111 x 1,11111 = 123456666,5

111111111 x 1,111111 = 123456777,7

111111111 x 1,1111111 = 123456788,8

111111111 x 1,11111111 = 123456789,9

111111111 x 1,111111111 = 123456790,0

Jeux

Sur une calculette, remplissez l'écran avec des 1. Multipliez par le nombre " 1, 111… " avec le maximum de 1. On obtient le nombre de Carroll, la suite des chiffres dans l'ordre, sauf le HUIT.

MOTIF AMUSANT
8 x 12345 679 = ( 987654321 – 9) 9 x 12345679 = (1111111111 – 10) Huit fois le nombre de Carroll égal le pannumérique retourné moins neuf. Neuf fois le nombre de Carroll égal le repunit d'ordre 10 moins dix.

Voir Nombres en 888…

CONJECTURE
Soit un nombre N = 123...n, en base n+1. Si on forme le produit de N par un multiplicateur inférieur à n et premier avec N, ce produit s'écrira avec les chiffres 1, 2, 3 ... n pris chacun une seule fois. Voir Conjecture

Fractions avec 81

0,12345679012345679012	= 10 / 81
0,24691358024691358025	= 20 / 81
0,37037037037037037037	= 30 / 81
0,49382716049382716049	= 40 / 81
0,61728395061728395062	= 50 / 81
0,74074074074074074074	= 60 / 81
0,86419753086419753086	= 70 / 81
0,98765432098765432099	= 80 / 81
1,11111111111111111111	= 90 / 81

Voir Fractions / Nombres permutations

Lewis Carroll (1832-1898)

Charles Lutwidge Dodgon ou Lewis Carroll: mathématicien, logicien, essayiste, photographe britannique. Ses œuvres:

Alice au pays des merveilles (1865)

De l'autre côté du miroir (1872)

La Chasse au Snark (1876)

Sylvie et Bruno (1886)

Logique sans peine ou Jeu de la logique (The Game of Logic) (1886)

Etc.

Voir Contemporains

Fractions qui engendrent presque tous les entiers
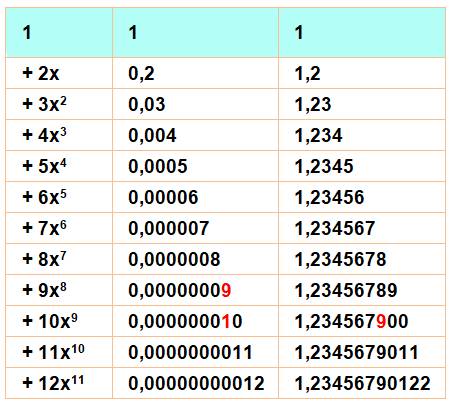
Ces fractions en 1/ (99…9k)^2 engendrent tous les nombres successifs jusqu'à 99…9k en omettant le nombre juste précédent: 99…98. Voir Pépites de nombres Explication Identité remarquable (développement de Taylor): Avec x = 0,1 la fraction vaut 1 / (1 – 0,1)² = 1 / (0,9)² = 1,2345679012345679012… Somme de gauche et mécanisme d'éjection du 8

Voir Autres fractions engendrant des suite de nombres

Suite	Puzzle de Lewis Carroll Snark de Carroll (mot-valise) De l'autre côté du miroir Développements périodiques remarquables Nombre 123 456 789 Nombre 142 857 Nombres magiques – Index Racine des nombres en 9999…
Voir	Consécutifs Jeux Motifs Nom des nombres Nombres décimaux en fractions Notation des grands nombres Rep-Digit Rep-Unit
Diconombre	Fraction 10/81 Nombre 1, 2… 10^7 Nombre 1,111 10^8 Nombre 8 Suite 0,123… Nombre 9 Nombre 99
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaNbExt/Carroll.htm