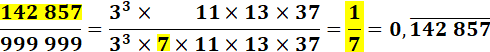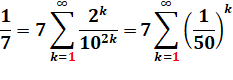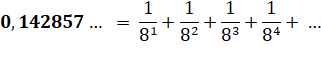|
|||||||||||||||||||||||||||||
![]()
|
Nombre 142 857
Curiosités et magie
avec ce nombre. Avec en prime:
|
|
|
||||||||||||||
|
Ce nombre est la période du
développement décimal de la fraction 1/7. Note: son
voisin du dessous présente un motif intéressant: 14 28 56. Chaque nouvelle
tranche de 2 est le double de celle qui précède. |
Ce nombre
est:
Voir Nom des nombres
/ |
|||||||||||||
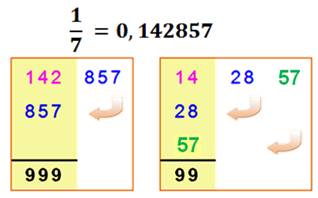
Loupe sur
la fraction 1/7
|
0, 142
857 142 857 … = 1/7 Période 14,
28 et 56 + 1 Sommes 142
+ 857 = 999 14
+ 28 + 57 = 99
|
Voir Développements |
|
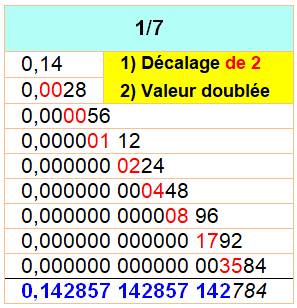
Formation des chiffres de 1/7
|
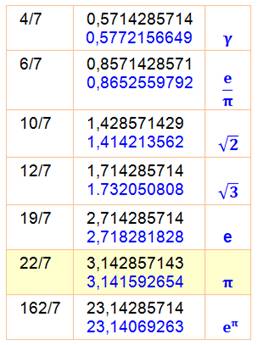
Approximations avec des
fractions en septièmes, dont 22/7
la célèbre
pour Pi. Ce sont
des coïncidences! |
Voir Nombre
0,142857 / Brève
de maths n°368
|
|
|
|
Nombre
à développement décimal périodique
142 857 x 1 = 142857 x 5 = 714285 x 4 = 571428 x 6 = 857142 x 2 = 285714 x 3 = 428571
Curiosité: fractions donnant les mêmes
chiffres: La plus petite: 27 / 64 = 0,421 875. La suivante: 153 / 320 = 0,478 125. Les deux qui suivent: 387 / 1600 = 0,241 875 et 1197 /
1600 = 0,748 125. Sur les 720 permutations possibles, 12 donnent un
dénominateur inférieur à 10 000. Les quatre indiquées plus huit en D = 8000. Merci
à JCB |
|
|
142857, têtu selon les
chiffres |
|
|
|
2 |
Manière de les calculer: Programme Mapple => |
|
|
5 |
|
|
|
8 |
|
|
|
9 |
1 + 4 + 2 + 8 + 5 + 7 = 27 => 9 14 + 28 + 57 = 99 142 + 857 = 999 142 857 x 7 = 999 999 |
|
|
10 |
10 = 1 x 7 + 3 100 = 14 x 7 + 2 1 000 = 142 x 7 + 6 10 000 = 1428 x 7 + 4 100 000 = 14285 x 7 + 5 1 000 000 = 142857 x 7 + 1 |
|
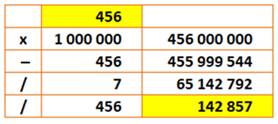
Un tour simple à exécuter avec une calculette
|
Choisis
un nombre jusqu'à un million Je
suis capable de trouver le résultat sans la calculette. 1) choisir
un nombre 2) le
multiplier par 1 million 3) soustraire
le nombre 4) diviser
par 7 5) diviser
par le nombre Le
résultat est toujours 142
857 |
Tableau des calculs avec l'exemple 456
Valable
pour des petits nombres comme des grands. |
|
|
|||||
|
Inscrire un nombre
de 5 chiffres sur un papier |
45 617 |
||||
|
Ajouter 142 857 |
+
142 857 = 188 474 |
||||
|
Multiplier par 7 |
x
7 = 1 319 318 |
||||
|
Barrer le chiffre
de gauche |
319
318 |
||||
|
Multiplier par 143 |
x
143 = 45 662 474 |
||||
|
Annoncer le chiffre |
45
662 474 |
||||
|
J'ajoute 143 |
+
143 = 45 662 617 |
||||
|
On retrouve le
nombre du départ avec les 2 premiers chiffres et les trois derniers |
45
xxx 617 |
||||
|
Explications
142 857 x 7 = 999 999 et 143 x 7
= 1 001.
Et,
un nombre fantôme va être introduit puis retranché: 999 999. |
|||||
|
Opérations |
Nombre à
deviner |
+ Nombre fantôme |
= Résultat |
||
|
Le nombre
ajouté |
45 617 |
142 857 |
188 474 |
||
|
Multiplication par
7 |
x 7 |
x 7 |
|
||
|
est multiplié pour
donner 100 000 – 1 |
319 319 |
999 999 |
1 319 318 |
||
|
et on soustrait 1
000 000 |
|
1 000 000 |
|
||
|
|
319 319 |
– 1 |
319 318 |
||
|
Multiplication par
143, après celle par 7 |
x 143 |
x 143 |
|
||
|
Le nombre initial
se retrouve multiplié par 7 x 143 = 1001 |
45 662 617 |
– 143 |
45 662 474 |
||
|
Il reste un résidu
parasite de 143 qu'il faut ajouter |
|
|
45 662 617 |
||
Voir Magie
|
|
|
|
Multiplications 142857 x 2 =
285714 x 3 =
428571 x 4 =
571428 x 5 =
714285 x 6 =
857142 x 7 = 999999 x 8 = 1142856 et 142856 + 1 = 142 857 x 9 = 1285713 et 285713 + 1 = 285714
142 857 x 1 = 142857 x 5 = 714285 x 4 = 571428 x 6 = 857142 x 2 = 285714 x 3 = 428571
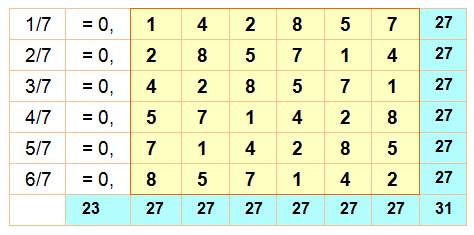
Même
si la moyenne est 27: 23 + 31 = 54 = 2 x 27 Voir Carrés
magiques aves les inverses des premiers Produits
avec des nombres plus élevés
Ex:
142 857 x 12 = 1 714
284 => 714 285 142 857 x 37 = 5 285 709 => 285 714
Ex:
142 857 x 84 = 11 999
988 => 999 999 |
|
|
Fractions
1
/7 = 0, 142857
142857 142857 2
/7 = 0, 285714 285714 285714 3
/7 = 0, 428571 428571 428571 4
/7 = 0, 571428 571428 571429 5
/7 = 0, 714285 714285 714286 6
/7 = 0, 857142 857142 857143 7
/7 = 1, 000000 000000 000000 8
/7 = 1, 142857 142857 142857 9
/7 = 1, 285714 285714 285714
Voir Nombre
têtus ou premiers longs en 142 857 Voir Nombres cycliques |
![]()
|
Nombre
magique et Pi 22
/7 = 3, 142857
142857 142857
Voir Valeurs
de Pi Et
l'inverse de ce nombre magique ? 1 / 142
857 = 0, 000 007
000 007 ... Voir Nombre
cyclique |
|
Nombre
magique pour sa multiplication
Exemple:
3 x 142 857 = 428 571
|
|
|
||
|
|
142 857 x 12 =
1 714 284
714 284 + 1 = 714 285 714 285 = 5 x 142 857 = (12 – 1 x 7)
x 142 857 |
|
|
|
142 857 x 493 = ? |
|
|
|
142 857 x (70 x 7 + 3) |
|
|
|
142 857 x 493 = 70 … |
|
|
|
142 857 x 3 = 428 571 |
|
|
|
142 857 x 493 = 70 428
571 – 70 = 70 428 501 |
|
|
|
142 857 x 378 = 142 857 x 54 x 7 = 142 857 x (53 x 7 + 7) = |
|
|
|
142 857 x 378 = 53 999 999 – 53 = 53
999 946 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
En
séparant le nombre en deux
Harshad 142 857 = 5 291 x (1 + 4 + 2 + 8 + 5
+ 7) Le
nombre magique 142 857 est divisible par la somme de ses chiffres. Voir
Nombre de Harshad Multiplications 142 857 = 11 x 12987 = 111 x 1287 = 1111 x 129 = 999999 x 7 = 9999 x 14 = 999 x 143 = 99 x 1443 = 9 x 15873 Progression
arithmétique Soit
les paires 18 45 et
27 tirées du nombre magique 142857.
|
|||||||||||||||||||||||||||||||||||||
![]()
|
142 857 2 = 20 408 122 449 et 20 408 + 122 449 =
142
857 142 857 3
= 2
915 443 148 696 793 et 2 915 + 443 148 + 696 793 = 1 142 856 En
ajoutant le 1 des millions aux unités, nous retrouvons notre nombre magique. 142 857 4
= 416
491 461 893 377 757 601 et 416+491461+893377+757601 = 2 142 855 C'est
en fait une propriété générale: le nombre magique 142 857, multiplié par un
nombre quelconque, donne un produit dont la somme des chiffres par bloc de
six est le nombre magique permuté. 142 857 x 123 = 17 571 411 et 17 + 571 411 = 571 428 Voir
Exploration / Nombre de Kaprekar Aussi
en morceaux 1422 = 20164 8572 = 734449 734449 – 20164 =
714285 |
![]()
Cette
dernière relation est générale: toute période d'un nombre décimal multiplié par
le nombre premier long
générateur est un repdigit en 9. Voir Autres exemples Également
avec cette dernière relation: 142
857 x 7 = 999 999 = (1 000 000 – 1) On
peut facilement calculer les multiples du nombre magique 142
857 x 7n = 1 000 000 n – n Enfin,
les multiples septième; pour les autres il faut diviser par sept. n
7 n . M N . M 1 999999 142857 2 1999998 285714 3 2999997 428571 4 3999996 571428 5 4999995 714285 6 5999994 857142 7 6999993 999999 8 7999992 1142856 9 8999991 1285713 Voir Calcul mental avec ce nombre Multiples
de 142857 142
857 x 367 = = 51 571 377 51 + 571 +
377 = 999 51 + 57 + 13
+ 77 = 198 => 99
(le 1
gauche est ajouté à droite) Tous
les multiples présentent ce genre de motif. |
![]()
Procédé qui fait apparaître
notre nombre magique. En
poursuivant le procédé, les 3 derniers chiffres seraient corrigés pour donner
la répétition de 142857: 1, 14 2, 1428 3, 14285 6 4, 142857 1 2 5, 142857 142 4 10,
142857 142857 14285568 15,
142857 142857 142857 142857 138176 20,
142857 142857 142857 142857 142857 1428421632 Cette
construction est valable pour tout nombre
périodique engendré par un nombre
premier long. La
même chose se retrouve avec les puissances de 5, ajoutées avec décalage.
Cette fois le nombre magique est engendré par la droite: 1,
3 57 (concaténation
de 35 = 7x5 et de 7) 2,
17 857 (357 + 35 x5 x 100 = 357 + 17500) 3,
892 857 4,
446 42857 5,
2232 142857 10,
6975446 42857 142857 15,
217982700892857 142857 142857 20,
681195940290 17857 142857 142857 142857 Modulo
9 et puissances de 2 et de 5
Idem avec les puissances de 5 modulo 9:
|
![]()
|
Voici
les vingt première itérations: 1 0, 12500000000000000000 2 0, 14062500000000000000 3 0, 14257812500000000000 4 0, 14282226562500000000 5 0, 14285278320312500000 6 0, 14285659790039062500 7 0, 14285707473754882812 8 0, 14285713434219360352 9 0, 14285714179277420044 10 0, 14285714272409677505 11 0, 14285714284051209688 12 0, 14285714285506401211 13 0, 14285714285688300151 14 0, 14285714285711037519 15 0, 14285714285713879690 16 0, 14285714285714234961 17 0, 14285714285714279370 18 0, 14285714285714284921 19 0, 14285714285714285615 20 0, 14285714285714285702 |
|
Il
est possible de créer les puissances de dix avec le nombre magique tronqué: 10 = 1 x 7 + 3 100 = 14 x 7 + 2 1 000 = 142 x 7 + 6 10 000 = 1428 x 7 + 4 100 000 = 14285 x 7 + 5 1 000 000 = 142857 x 7 + 1 |
|
|
|
|
Parmi
toutes les permutations du nombre magique M = 142857, combien donnent un repdigit lorsqu'ils sont divisés par un diviseur de M? N Diviseur Quotient N/D 142857 47619 3 285714 47619 6 142857 15873 9 428571 47619 9 142857 12987 11 241758 10989 22 285714 12987 22 142857 4329 33 428571 12987 33 571428 12987 44 714285 12987 55 241758 3663 66 285714 4329 66 857142 12987 66 142857 1443 99 428571 4329 99 147852 1332 111 142857 1287 111 428571 3861 111 285714 1287 222 857142 3861 222 142857 429 333 428571 1287 333 147852 333 444 571428 1287 444 714285 1287 555 285714 429 666 857142 1287 666 258741 333 777 142857 143 999 428571 429 999 En
majorité, on retrouve les permutations
circulaires de 142857 (rouge); mais aussi, les permutations circulaires
de ce nombre lues dans l'autre sens758241. Rappel: Ce
nombre à six chiffres et chaque chiffre vaut l'une des six valeurs {1, 2, 4,
5, 7, 8}. Cinq chiffres étant fixés, le dernier peut
prendre 6 valeurs. Quatre chiffres étant fixés, le cinquième
peut prendre 6
valeurs; ce qui veut dire que les deux derniers peuvent prendre 6x6 valeurs Trois chiffres étant fixés, les trois
derniers peuvent prendre 6x6x6 = 63 valeurs. Pour les chiffres, nous avons donc 66 = 46 656
valeurs dont 31 correspondent à nos conditions. Voir p-liste |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le nombre magique
142 857, multiplié par un nombre quelconque, donne un produit dont la somme
des chiffres par bloc de six est le nombre magique permuté. Exploration
Observez
Avec
n autour de 1 000
Avec
n autour de 1 000 000 000 Note :
08 signifie une succession de 8 zéros
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Merci à Richard Lefébvre pour sa relecture
attentive
Voir son
superbe XModulorama animé
![]()
|
Suite |
|
|
Voir |
|
|
DiciNombre |
|
|
Cette page |
![]()