|
|||||||||||||||||||||||||||||||
![]()
|
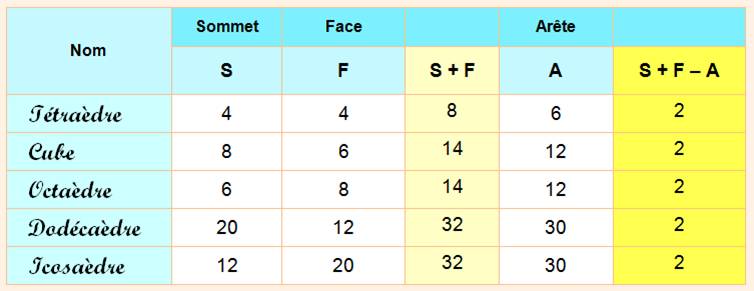
INVARIANT des corps en TOPOLOGIE Descartes puis Euler ont
découvert que les polyèdres convexes avaient le nombre 2 comme invariant.
Cette forme d'invariant se
généralise aux polyèdres creux et aux corps de toutes sortes. La valeur de la
somme est telle qu'elle constitue une caractéristique
permettant de classer les corps. |
Anglais: Euler'sFormula
/ Euler's Polygonal Formula
Voir Théorème
de Descartes-Euler
|
|
|
|
|
|
Voir Mnémotechnique
D'après La conjecture de Poincaré – George G.
Szpiro – Lattès Points sciences – 2007 – pages 89 à
93
|
|
||
|
|
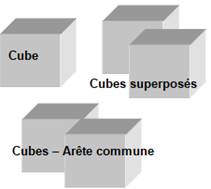
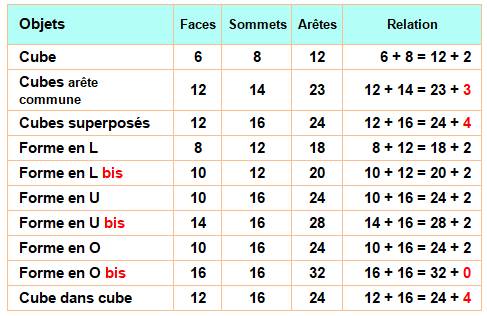
Avec le cube,
ou le pavé quelconque, on retrouve la relation d'Euler. Ajoutez un cube
superposé ou avec une arête commune et la relation n'est plus vérifiés. Avec
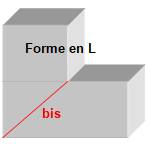
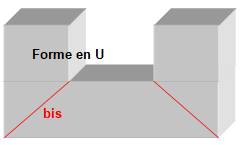
les formes en L ou en U, la relation est vérifiée dans les deux cas suivants:
La
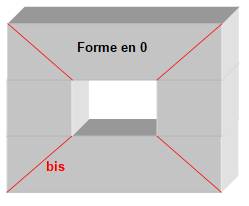
situation est plus étrange avec la forme en O (cube troué ou donut cubique).
Avec
un cube enfouit à l'intérieur d'un cube, l'invariant vaut 4. |
|
Avec ce volume en forme
de cube troué, l'invariant d'Euler pour forme trouée est vérifié.
F + S = A + 0 ![]() 16 + 16 = 32 + 0
16 + 16 = 32 + 0

(Rebords
des structures non pris en compte)
Voir Arche de la
Défense et hypercube
|
|
|
|
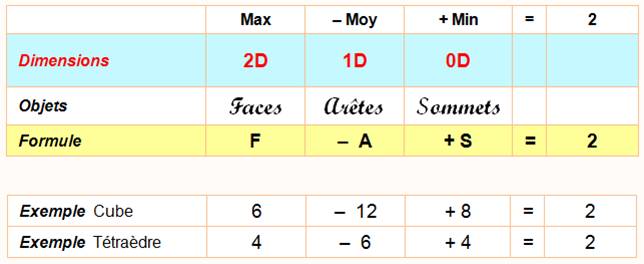
Exemples
Analogies
|
|
|
|
||
|
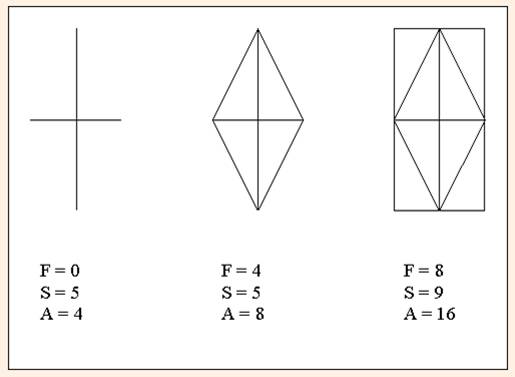
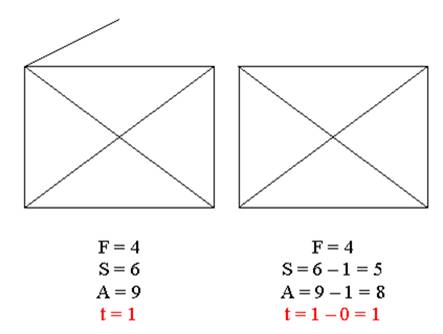
Suppression des
éléments les uns après les autres.
F –
A + S = 1 |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/RelEuler.htm |
![]()