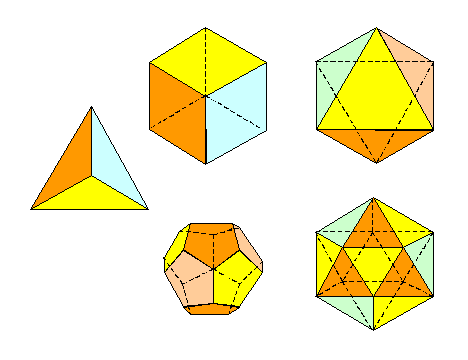|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
POLYÈDRES Volumes
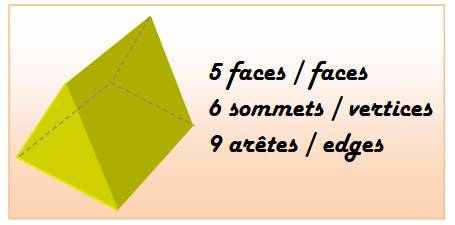
très nombreux. Sauf lorsqu'ils sont réguliers ou semi-réguliers. Polyèdre: solide ayant pour frontière des polygones
plans appelés faces ou facettes, dont les côtés communs sont les arêtes qui
se rejoignent aux sommets Ils sont
convexes ou concaves; réguliers, semi-réguliers ou quelconques. Il n'existe
que cinq polyèdres réguliers convexes. |
Dodécicosidodécaèdre |
Anglais: one polyhedron - Pluriel:
many polyhedra
Vocabulaire
|
|
||
|
Polyèdre
|
|
|
|
Polyèdre
uniforme
|
Nom
et visualisation des 75 + 5, voir Visual Index of all Uniform Polyhedra |
|
|
Polyèdre
convexe
|
|
|
|
Polyèdre
semi-régulier
|
|
|
|
Polyèdre
régulier
|
|
|
|
Nomenclature résumée |
|
||
|
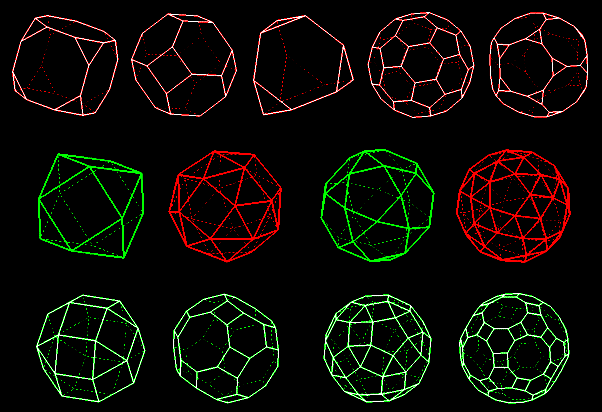
75 polyèdres uniformes et une
infinité de prismes et anti-prismes |
|||
|
|
Convexes |
Non-convexes |
|
|
9 réguliers |
5 solides Platoniciens |
4 solides de Poinsot-Kepler |
|
|
15 quasi-réguliers |
2 solides Archimédiens |
13 |
|
|
51+ semi-réguliers |
11
solides Archimédiens |
17 solides
Archimédiens étoilés |
|
|
|
infinité
de prismes et anti-prismes |
23 autres |
|
En savoir
plus: SITE Polyèdre - Wikipédia et
aussi le même en langue anglaises;
voir les
liens qui y sont indiqués
|
ou
SOLIDES PLATONICIENS |
|
|
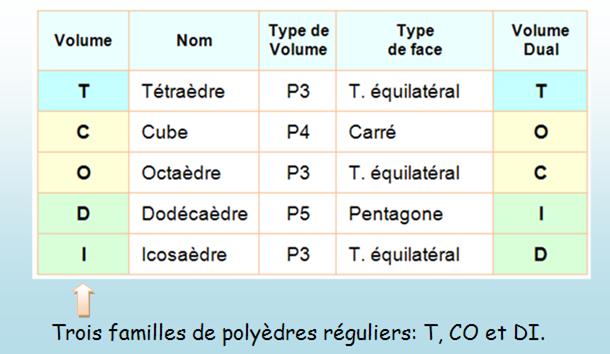
Il n'y a que cinq
polyèdres réguliers.
|
|
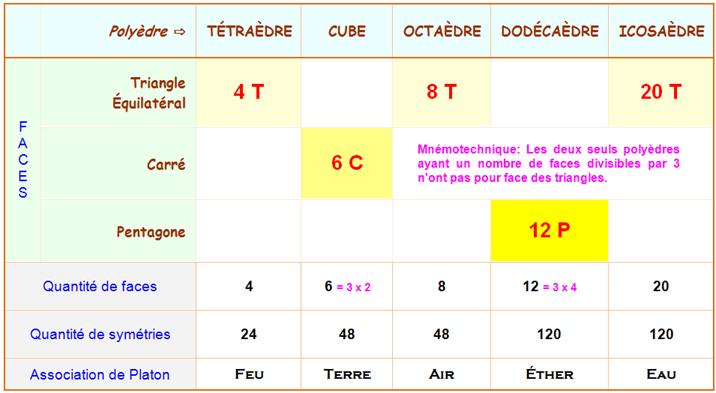
Voir Triangle
équilatéral / Tétraèdre / Carré / Pentagone / Cube
/ Octaèdre / Dodécaèdre / Icosaèdre / Mnémotechnique
|
À
l'origine deux catégories de triangles:
Avec
ces triangles, il forme les polyèdres
La
transmutation consiste à modifier ces arrangements, pense Platon. |
|
|
||||||||||||||||||||||||||||
|
Observation
Théorème de
Descartes-Euler S + F = A + 2 Voir Développements / Euler
|
||||||||||||||||||||||||||||
Voir Formule
pour Polytopes / Pour
les graphes / Théorème
des quatre couleurs
|
|
|||||||
|
Volume dual
Voir Dualité
Voir Symétrie
Dualité
Voir
Cuboctaèdre |
|||||||
|
|
|
|
Kepler et Pythagore
Modèle proposé dans
son ouvrage " Le Mystère cosmique " – 1596 |
|
Voir Planètes / Astronomie / Pythagore
|
|
||||||||||||||||
|
Billard volumique
Il existe au moins
une trajectoire pour
|
||||||||||||||||
|
|
|
|
Il existe
exactement 92 polyèdres convexes avec des
faces polygonales régulières (et pas nécessairement des sommets équivalents).
Ils sont connus sous le nom de solides de Johnson.
Les polyèdres avec
des sommets identiques reliés par une opération de symétrie sont connus sous
le nom de polyèdres uniformes. Il existe
75 polyèdres de ce type dans lesquels seules deux faces peuvent se rencontrer
sur un bord, et 76 dans lesquels un nombre pair de faces peut se rencontrer. Parmi ceux-ci, 37
ont été découverts par Badoureau en 1881 et 12 par Coxeter et Miller vers
1930. |
|
|
|
|||||
|
Nom |
Polyèdre
de base |
Modification |
Nb. de faces |
Faces |
|
|
|
|
adouci |
8 |
4 triangles 4 hexagones |
|
|
Dymaxion |
|
tronqué |
14 |
6 carrés 8 triangles |
|
|
|
|
adouci |
14 |
6 octogones 8 triangles |
|
|
|
|
adouci |
14 |
8 hexagones 6 carrés |
|
|
Petit
rhombicuboctaèdre |
|
tronqué |
26 |
18 carrés 8 triangles |
|
|
Grand
rhombicuboctaèdre |
|
adouci |
26 |
6 octogones 8 hexagones 12 carrés |
|
|
|
|
tronqué |
32 |
12 décagones 20 triangles |
|
|
Icosidodécaèdre |
|
adouci |
32 |
12 pentagones 20 triangles |
|
|
Icosaèdre tronqué |
|
adouci |
32 |
12 pentagones 20 hexagones |
|
|
|
|
transformé |
38 |
6 carrés 32 triangles |
|
|
Petit
Rhombicosidodécaèdre |
|
tronqué |
62 |
12 pentagones 30 carrés 20 triangles |
|
|
Grand
Rhombicosidodécaèdre |
|
adouci |
62 |
12 décagones 20 hexagones 30 carrés |
|
|
|
|
transformé |
92 |
12 pentagones 80 triangles |
|
|
|
|||||||||||||
|
|
|||||||||||||
Voir The Fifty-Nine
Icosahedra – H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie
|
|
||
|
Le
calcul de l’enveloppe convexe d’un
ensemble de points dans l’espace est un des calculs les plus ardus de la
géométrie par ordinateur. Pour un ensemble
de points dans le plan, l’enveloppe correspond au périmètre d’un élastique
engobant tous ces points. Dans
l’espace, il faut imaginer un emballage qui contiendrait tous les points |
The Convex Hull is one of the more researched problems of
Computational Geometry. The Graham Scan is one of the simpler convex hull
algorithms, but certainly not the only one.
|
|
![]()
|
Voir |
|
|
Diconombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Polyedre.htm |
|
Sites |
Animation des polyèdres
Réguliers
Semi-réguliers Divers
Éducation et Patrons
La formule d'Euler |
![]()