NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/08/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Géométrie
Débutants Géométrie	TOPOLOGIE			Glossaire Topologie
INDEX Topologie	Conjecture de Poincaré	Caractéristique d'Euler-Poincaré	Outils de la topologie
	Sommaire de cette page >>> Approche >>> Contraction >>> Décomposition >>> Décomposition en objets de base >>> Sphère >>> Tore- Surface >>> Boule et Tore 3D >>> Bilan

TOPOLOGIE

Caractéristique d'Euler-Poincaré

Comment classer les objets selon leur forme pour les organiser en familles, en classes, de manière à en déduire des propriétés communes?

Voici quelques idées pour approcher ce sujet.

APPROCHE
Le théorème de Descartes-Euler caractérise les polyèdres. Le nombre k est un invariant pour tout polyèdre. En topologie, est-il possible de trouver un tel invariant? Ou, en tout cas, un nombre qui caractérise des familles d'objets ayant les mêmes caractéristiques. L'idée consiste à décomposer l'objet en éléments de base, selon une règle, et compter ces éléments selon leur dimension: points (Dim. 0), segments (Dim. 1), surfaces (Dim. 2), volumes (Dim. 3), hyper-volumes (Dim. 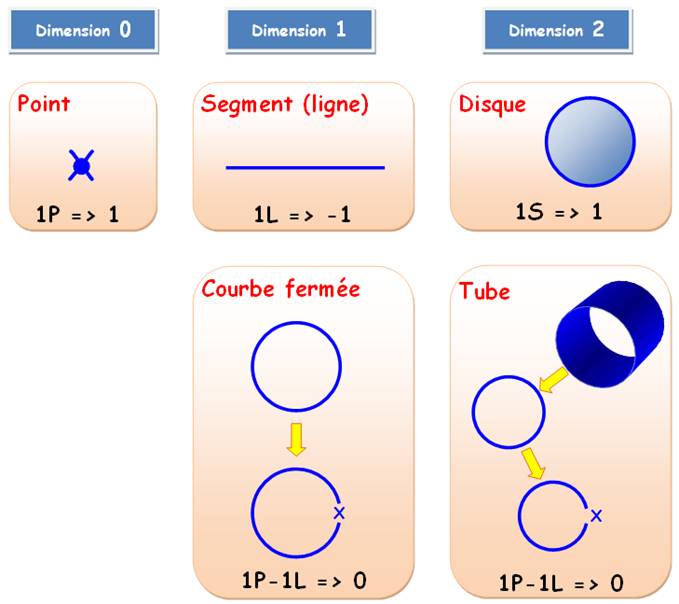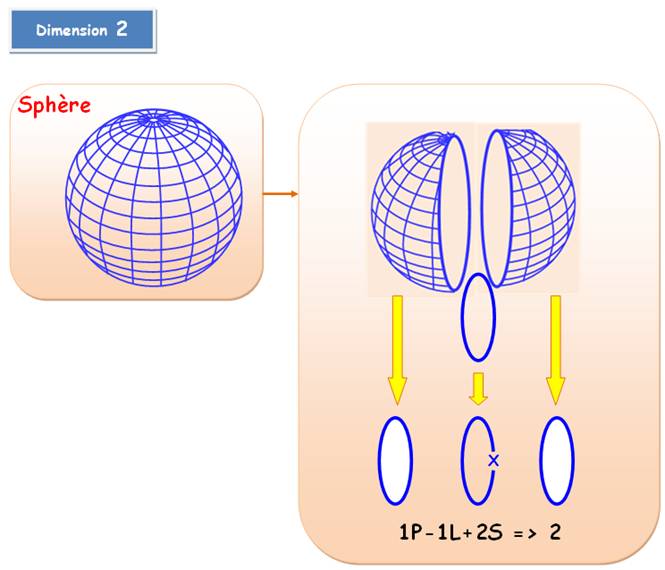4) …	Polyèdres: Relation d'Euler k = F + S – A = 2 Faces + Sommets - Arêtes = 2 Objets topologiques: Caractéristique d'Euler-Poincaré k = P – L + S – V … Points – Lignes (segments) + Surfaces – Volumes … Comment définir ces objets précisément?

Contraction
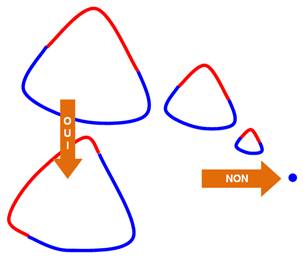
Analogie L'idée consiste à prendre un objet et à le contracter au maximum sur lui-même, dans son propre espace. Imaginez un segment personnalisé sous la forme d'un ver de terre. Effrayé, il se contracte sur lui-même. Ses anneaux s'entassent les uns sur les autres comme un ressort comprimé. Terrorisé, il se replie dans ses anneaux pour ne POINT être vu! En topologie Un segment, un bout de courbe, se contracte le long de sa propre courbe pour terminer en un seul point. Cette manière de se contracter est un principe général en topologie.	Contractions: Courbe ouverte => Point Tuyau => Cercle

Décomposition
Nous venons de voir qu'une courbe ouverte se contracte en un point. Et la courbe fermée? On se souvient de la règle: elle doit se contracter sur elle-même, sur sa propre trace. Il est possible de la faire tourner sur son sillage, mais … Impossible de la rétrécir à un seul point. La taille de la boucle peut être réduite autant que l'on veut. Elle devient une minuscule boucle. Elle approche la taille d'un point. Mais, pour devenir un point, il faudrait coller (coudre) les bords entre eux, faire une sorte de rupture (collapse) qui n'est pas autorisée. Alors, que faire de la courbe fermée? La couper par un coup de ciseaux ? Oui. Mais alors nous devons matérialiser le coup de ciseaux par un point et, il restera une courbe ouverte, deux éléments de base de la topologie. 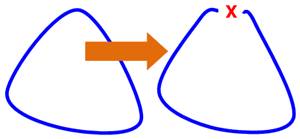Note: La courbe ouverte obtenue est un élément de base de dimension 1; elle est témoin de cette dimension. Elle ne peut pas être contractée.	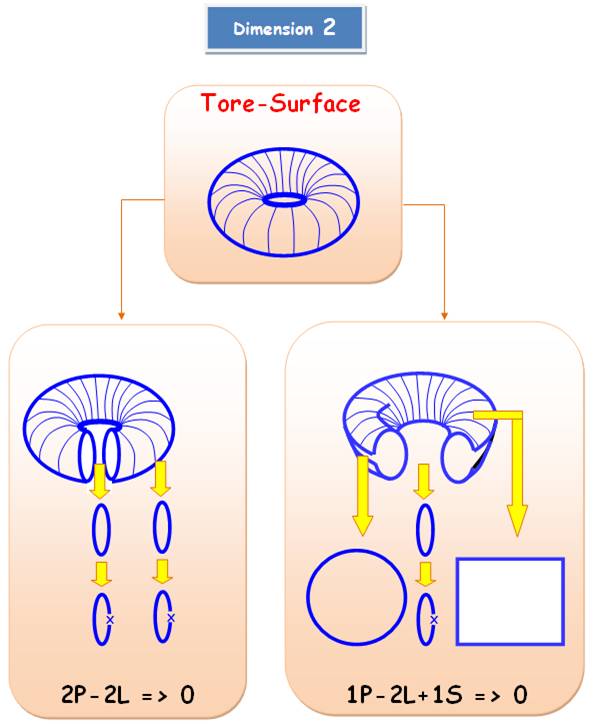Une courbe ouverte peut se contracter en un point. Ce n'est pas le cas pour une courbe fermée. Mais, peut-on la décomposer? Oui! La courbe fermée se décompose en deux éléments de base: Un point – dimension 0, et Un segment – dimension 1.

Décomposition en objets de base
Les éléments de base sont: le point (P), le segment, le bout de courbe ou le bout de ligne (L), le disque, la feuille de papier ou la surface (S), etc. Cette illustration montre les objets, leur dimension et, en bas, la caractéristique d'Euler- Poincaré: P – L + S. Les objets où figure une flèche jaune sont contractiles.

Sphère – Coquille – S2
La sphère est la surface de la boule, comme ce qu'est la coquille à l'œuf. C'est une surface de dimension 2 qui flotte dans un espace de dimension 3. Sa décomposition nécessite trois éléments de base: Coupée en deux, elle produit deux demi-coquilles qui sont ces surfaces. La trace de la coupe est un cercle qui se décompose lui-même en un segment et un point.

Tore – Surface
La surface du tore, sa coquille, peut se décomposer de deux manières. La caractéristique est égale à 0 dans les deux cas. C'est une propriété de cette indicateur: sa valeur est la même quelle que soit la manière de décomposer l'objet.

Boule et tore en trois dimensions
La boule, sphère pleine, se contracte en une petite sphère; C'est un élément de base. Le tore, comme le cercle, ne se contracte pas. Il faut les couper pour les décompose en un volume, topologiquement équivalent à la sphère, et un disque, trace de la coupe du tore.

BILAN

Les objets se contractent pour aboutir à un élément de base, ou se décomposent en éléments de base.

Quelle que soit la décomposition d'un objet, sa caractéristique d'Euler-Poincaré (CEP) est constante.

Dim.	Objet	CEP	Base
0	Point	1	OUI
1	Segment ouvert	– 1	OUI
1	Cercle	0
2	Disque	1
2	Tube	0
2	Sphère	2
2	Tore	0
3	Boule	-1	OUI
3	Tore	0

Tout l'intérêt réside dans l'exploitation de cette caractéristique pour des dimensions supérieures.

C'est le cas aussi pour les objets très torturés. Le but étant de les simplifier; comme vous le feriez en présence d'une corde emmêlée dont vous essaieriez de distinguer les nœuds véritables des simples boucles.

Parfois, il est utile de réunir deux objets pour obtenir un nouvel objet topologique dont l'étude présente un intérêt particulier.

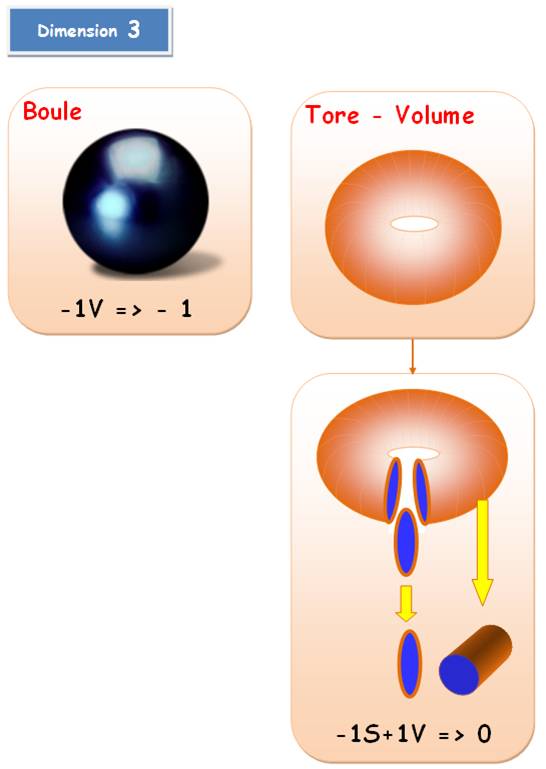
Exemple de cette chirurgie: prenez deux tores (chambres à air); découpez une rustine sur chacun; vous les écartez; chaque tore est percé d'un trou; cousez les bords de ces trous ensemble pour réunir les deux tores. Vous obtenez un bretzel à deux ouvertures.

Pour arriver à démontrer la conjecture de Poincaré, une panoplie d'outils de ce genre a été mise au point par une pléiade de mathématiciens, chacun persuadé de réussir.

Suite	Outils de la topologie Quatre couleurs Topologie – Index
Voir	Couleurs Ensemble
DicoNombre	Nombre 2
Site	Travaux d'élèves reprenant les infos de cette page
Bande dessinée	Le Topologicon – Lanturlu Une vulgarisation de la topologie en bande dessinée écrite par Jean-Pierre Petit
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/IndicEP.htm