NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/03/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Outils mathématiques
Débutants Général	GROUPES			Glossaire Symétrie
INDEX Structures algébriques Géométrie	Introduction	Triangles et carrés	Groupe – Définition	Symétrie
		1D - Bande	2D - Papier peint	3D - Cristallographie
		Sommaire de cette page >>> Les symétries du triangle >>> Les symétries du carré >>> Les symétries du polygone régulier >>> Groupe

SYMÉTRIES et GROUPES

Groupes diédraux

Exemples géométriques avec les symétries des triangles équilatéraux, des carrés et des polygones réguliers.

Les symétries du triangle

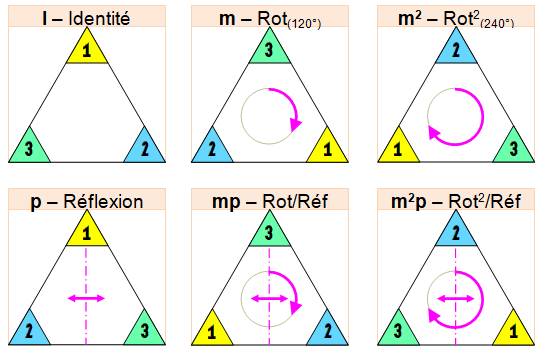
Prenons un triangle équilatéral. Cherchons tous les cas possibles de modifications (transformations) sans changer la forme du triangle: Il y en 2 par rotation de 120° et Il y en a 3 par symétrie (miroir) par rapport à chacune des hauteurs. Total 6 pour un triangle à 3 côtés. Avec les noms de baptême indiqués ci-dessus: m une rotation de 120° dans le sens des aiguilles d'une montre; p une réflexion par rapport à une droite verticale passant par le centre. 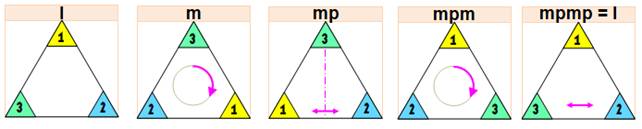Par exemple: la transformation mp est une rotation (figure 2), suivie d'une réflexion verticale qui inverse la base (figure 5). Les figues du bas sont exactement celles du haut avec inversion des nombres de la base. Six transformations: trois cas avec 1, 2 ou 3 en haut et deux sous-cas avec l'inversion de la base => 3 x 2 = 6 cas. 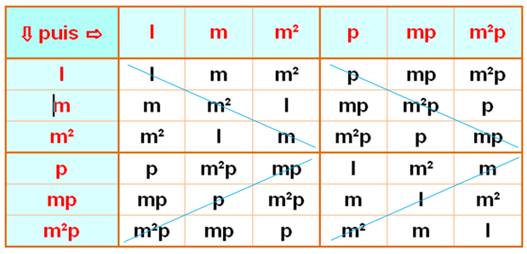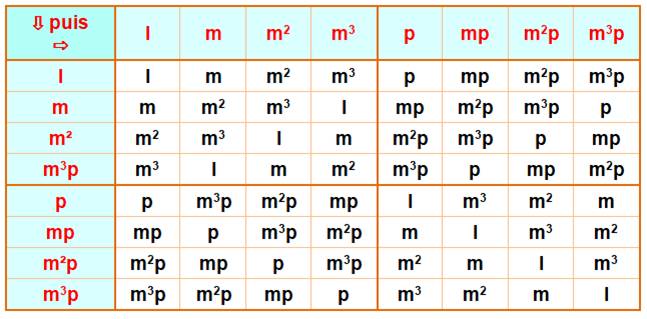Exemple de composition de transformations Toutes les compositions possibles Voyons toutes les combinaisons d'opérations deux à deux. L'opération résultante est l'une des opérations initiales. On note également la formation de quatre sous-groupes (régions 3 x 3). Groupe diédral d'ordre 6 Attention: les transformations ne sont pas commutatives; elles dépendent de l'ordre dans lequel elles sont effectuées. Les quatre sous-groupes sont donc différents avec cependant une symétrie interne par rapport à une des diagonales. Trois rotations de 120° redonnent la configuration de départ: m^3 = I. De même pour deux réflexions par rapport à une ligne horizontale: p² = I. Et aussi pour deux réflexions par rapport à une diagonale: (mp) (mp) = I.

Merci à Jacques Pellet pour ses remarques

Les symétries du carré

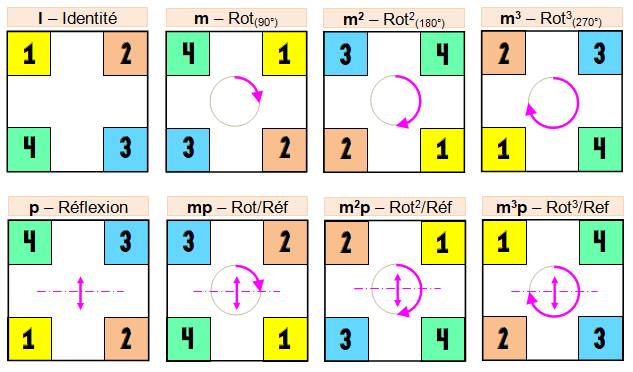
Prenons un carré. Cherchons tous les cas possibles de modifications sans changer la forme du carré: Il y en 3 par rotation de 90°; et Il y en a 4 par symétrie par rapport à chacune des médianes et diagonales. Total 8 pour un carré à 4 côtés. Groupe diédral d'ordre 8 Quatre rotations de 90° redonnent la configuration de départ: m^4 = I. De même pour deux réflexions par rapport à une ligne horizontale: p² = I. Et aussi pour deux réflexions par rapport à une diagonale: (mp) (mp) = I.

Les symétries du polygone régulier
Un polygone régulier à n côtés forme un groupe de symétrie à 2n éléments. En termes mathématiques ces groupes sont dits diédraux d'ordre 2n. Avec m^n = I p² = I et (mp) (mp) = I.

Suite en Symétrie des polygones

GROUPE – Caractéristiques

Toutes les composées possibles font parties de l'ensemble des éléments de départ: le groupe est fermé. L'élément I, appliqué à une ligne ou à une colonne, redonne le même élément. C'est l'élément identité. L'élément I apparaît une fois dans chaque ligne et chaque colonne. Il existe une fonction, dite inverse, qui couple deux éléments pour donner l'identité. Ceci existe pour tout couple et de manière unique. Les couplages sont associatifs. On peut faire des combinaisons de couplages dans l'ordre que l'on veut. Exemple: mmp = m(mp) = (mm)p = m²p Ces quatre propriétés définissent un GROUPE (au sens mathématique).

Retour	Symétrie
Suite	Groupe – Définition 1D - Bande Symétrie des étoiles à six branches Symétrie – Glossaire
Voir	DicoMot Géométrie – Index Illusions d'optique Constructions des ensembles de nombres Polyèdres Transformation Triangles
Sites	Groupe diédral – Wkipédia Dihedral group –Wikipedia – Plus illustré que le site français Groupe diédral – Bibm@th.net Introduction à la théorie des groupes – Université de Toulouse Dihedral group – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/SymGroup.htm