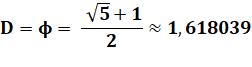Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/07/2022 M'écrire Brèves de Maths

INDEX Types de nombres	TRAPÈZE
	Quadrilatère	Trapèze	Trapèze et pentagone

Faites un double-clic pour un retour en haut de page

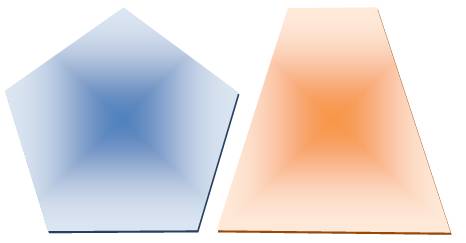
Trapèze et pentagone Dissection en triangles isocèles Transformer un trapèze isocèle en pentagone régulier par découpage de quatre triangles isocèles.
	Sommaire de cette page >>> Dissection >>> Mesures	Débutants Nombres Glossaire Nombres

Dissection		haut
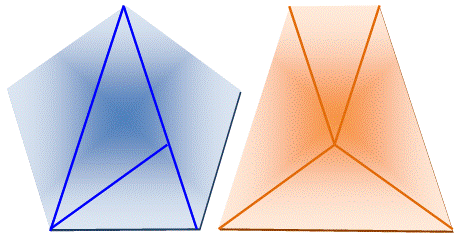
Énigme Découpez le pentagone régulier en quatre triangles isocèles, et Formez un trapèze isocèle. Solution Les triangles isocèles ne sont pas tous les quatre de la même taille. La base et les côtés du trapèze ont même mesure et c'est celle des diagonales du pentagone, soit le nombre d'or pour un pentagone de côté unité

Les mesures		haut
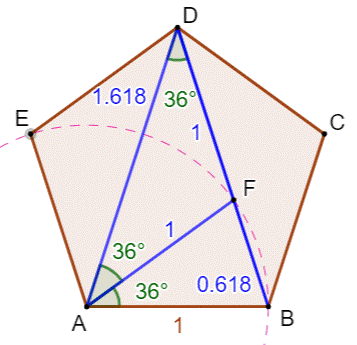
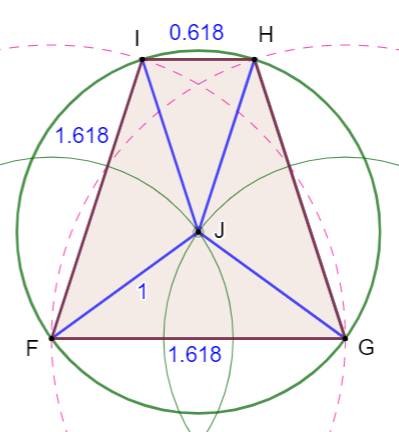
Pentagone régulier Avec un côté égal à 1, les diagonales valent le nombre d'or: Le triangle ABF doit être isocèle. Ses côtés égaux mesurent 1. Sur la diagonale AD, on construit le triangle isocèle ADF dont les côtés de même mesure valent 1. Alors, la base BF du triangle isocèle ABF mesure: Trapèze isocèle On construit FG = nombre d'or = . Cercles de centres F et G et de rayon unité. Cercles de centres F et G et de rayon . Intersection J, centre du cercle circonscrit vert. Intersections H et I. Trapèze isocèle FGHI.

Haut de page

Retour	Trapèze
Suite	Centre de gravité du trapèze isocèle Rectangle Trapèze converti en hexagone Triangles Parallélogramme
Voir	4 Couleurs Carré dans le triangle Constructions avec des allumettes Géométrie – Index Jeux – Index Nombres Carrés Parallélogramme dans le cube Pavage du carré Polygones Somme de vecteurs
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/TrapPent.htm