Bases de la géométrie dans l'espace

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/03/2022 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Géométrie dans l'espace
Débutants Géométrie	Bases				Glossaire Géométrie
INDEX Géométrie Constructions		Plan	Orthogonalité	Trois perpendiculaires
		Sommaire de cette page >>> Définition >>> Points coplanaires >>> Partages >>> Position >>> Plan sécant >>> Bilan

Le PLAN

Rappel des rudiments.

Les plans qui se croisent, les droites qui se coupent.

Définition
Le plan (ou surface plane) est une surface telle que si elle contient deux point d'une droite, elle contient la droite toute entière. Définition mathématique du plan: variété linéaire affine ou projective de dimension 2. Anglais: a plane is a surface such, that if any two points are taken in it, the straight line joining them lies wholly in the surface. Une surface courbe n'est ni plane, ni composée de surfaces planes.	Métaphore Si tu te tiens debout et que tu mets deux orteils dans l'eau, tu plonges complètement dans l'eau! Exemples Un beau miroir donne une idée du plan; La surface immobile de l'eau (plan horizontal, en plus); La surface du bureau; Un mur de plâtre; Le tapis du billard; Une surface lisse en marbre; etc. Une surface non plane est dite gauche. Rendue plane, elle est dressée. En menuiserie une dégauchisseuse sert à dresser un morceau de bois, à obtenir des faces les plus planes possibles.
Le plan (P): est illimité dans toutes les directions (même si sa représentation sous forme d'un parallélogramme est limitée); peut glisser sur lui-même; est égal à tout plan. La droite (D), définie par les point M et M' du plan, est totalement contenue dans le plan P.

Points coplanaires

Par un point ou deux points passe une infinité de plans.

Mais, trois points définissent un plan précis.

Un tabouret est toujours stable même si le sol n'est pas parfaitement plat.

Un triangle est contenu dans un plan.

Par trois points passent deux droites qui se coupent. Alors, deux droites qui se coupent définissent un plan. De même pour une droite et un point extérieur.

Quatre points ou plus ne sont généralement pas dans un plan. S'ils le sont, ils sont dits coplanaires.

Une table ne trouvera pas naturellement sa stabilité sauf sur un sol extrêmement plat. Souvent, les pattes sont munies d'une extrémité ajustable par un pas de vis pour permettre de caler la table.

Un quadrilatère n'est pas forcément contenu dans un plan. Il suffit de la plier selon une diagonale pour s'en rendre compte.

Le tabouret est toujours stable. La table est stable sur sol plat ou à condition de caler la quatrième patte.

Les cinq roulettes du fauteuil définissent une zone au sol suffisamment grande pour donner de la stabilité*. Elles n'échappent pas à la règle de coplanarité. Le fauteuil doit circuler sur un sol de bureau bien plat.

*Plus la surface au sol est grande plus la verticale du centre de gravité a de chance de tomber dans cette zone dite polygone de sustentation.

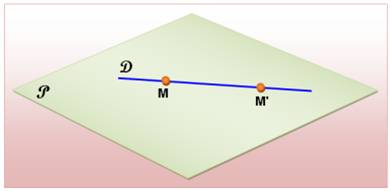
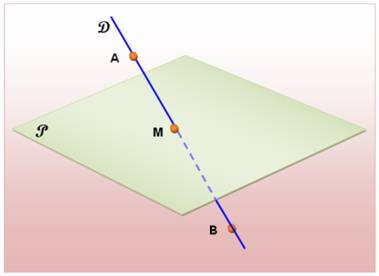
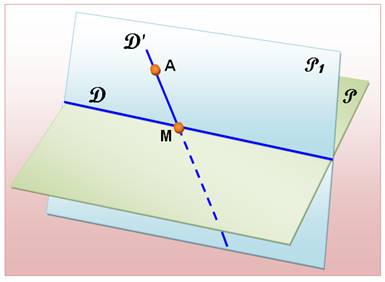
Partages et intersections uniques

Le plan partage l’espace en deux régions appelées demi-espace.

Deux points (A et B), chacun dans un demi-espace, définissent une droite (D) qui traverse (coupe) le plan. Elle rencontre le plan en un point unique (M).

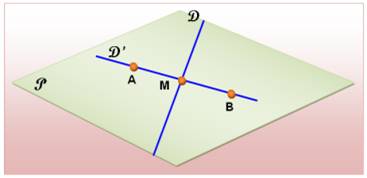
Une droite (D) du plan partage le plan en deux demi-plans.

Deux points (A et B), chacun dans un demi-plan, définissent une droite (D') qui coupe la droite D en un point unique (M).

Positions

Deux plans (P et P') qui ne se rencontrent jamais sont dits parallèles.

Une droite (D) et un plan (P) sont parallèles s'ils ne se coupent jamais.

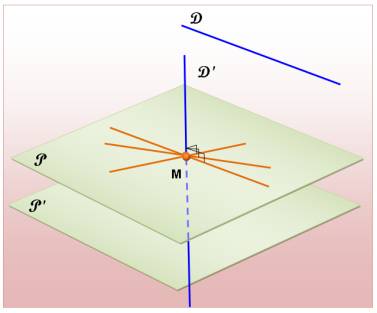
Cette propriété vaut pour le plan P' qui est parallèle à P.

Une droite (D') est perpendiculaire à un plan (P) si elle est perpendiculaire à toutes les droites (brunes) du plan qu'elle rencontre.

Cette propriété vaut pour le plan P' qui est parallèle à P.

Deux droites du plan sont concourantes en M. Si une droite est perpendiculaire en M à ces deux droites, elle est perpendiculaire au plan.

Une droite perpendiculaire à un plan. Toute parallèle à cette droite est perpendiculaire au plan.

Un plan est vertical s'il passe par la droite formée par le fil à plomb.

Un plan est horizontal s'il est perpendiculaire à cette droite du fil à plomb.

Si deux droites sont perpendiculaires à un plan, elles sont parallèles.

Par rapport à un plan, une droite peut:

appartenir au plan
infinité de points en commun;

couper le plan (en position perpendiculaire ou quelconque),
un seul point en commun; ou

être parallèle au plan.
aucun point en commun.

De même deux droites peuvent:

se couper

elles sont coplanaires;

être parallèles

elles sont coplanaires;

ne jamais se rencontre sans être parallèles

elles ne sont pas coplanaires. Elles sont en oblique (skew en anglais).

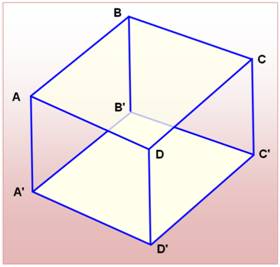
Le plan ABB'A' coupe les plans ABCD et A'B'C'D' selon deux droites parallèles AB et A'B'.

Les droites AB et DD' ne se rencontrent jamais.

Deux droites qui se coupent forment un plan et un seul.

Avec la droite D nous créons le plan P que nous faisons tourner autour de D, comme autour d'une charnière.

Nous nous arrêtons en position P₁, lorsque le plan contient le point A de D'. C'est toujours possible.

Le point A appartient à P; de même que le point M par construction. Tous les points de la droite D portant le segment AB sont donc dans le plan P₁.

Deux plans se coupent selon une droite.

Plan-plan
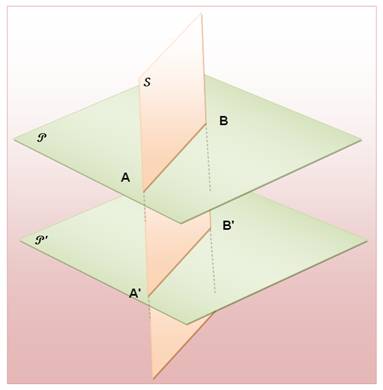
Une propriété essentielle! Un plan sécant (S) à deux plans parallèles (P et P') crée deux lignes d'intersection (AB et A'B') qui sont parallèles. La preuve est très simple: AB et A'B' sont chacun dans des plans P et P' qui ne se rencontrent jamais; Or, AB et A'B' sont dans le même plan; Conclusion: AB et A'B' sont parallèles. Anglais: if two parallel planes are cut by a third plane, their lines of section with it are parallel.
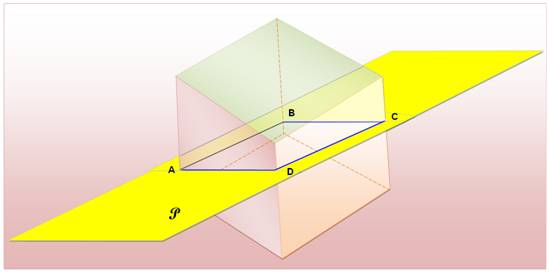
Application au cube Tout plan sécant P, traversant deux faces d'un cube, dessinent sur ces faces deux segments parallèles. De sorte que le quadrilatère ABCD est un parallélogramme.