|
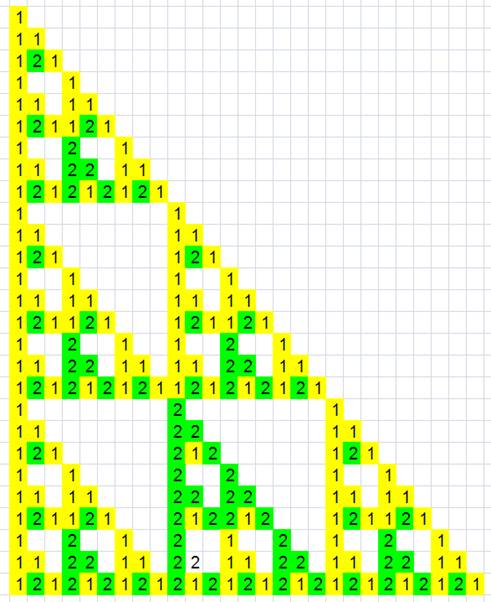
 En poursuivant cette façon de faire, la figure suivante se forme: En poursuivant cette façon de faire, la figure suivante se forme:

 Imaginez un lissage des bords anguleux (comme si nous regardions de
loin). Vous aurez des triangles qui forment le triangle
ou napperon fractal de Sierpinski. Imaginez un lissage des bords anguleux (comme si nous regardions de
loin). Vous aurez des triangles qui forment le triangle
ou napperon fractal de Sierpinski.
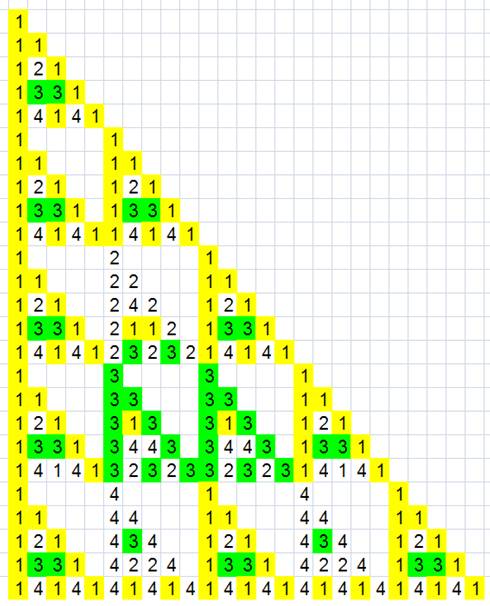
 La construction est la suivante: La construction est la suivante:
 Départ: le très grand triangle; Départ: le très grand triangle;
 Un triangle quatre fois plus petit est évidé au centre; il reste trois
triangles identiques sur les sommets Un triangle quatre fois plus petit est évidé au centre; il reste trois
triangles identiques sur les sommets
 Chacun de ces trois triangles subit le même sort que le grand triangle
initial: évidé d'un quart au centre. Chacun de ces trois triangles subit le même sort que le grand triangle
initial: évidé d'un quart au centre.
 Même procédure autant que vous voulez. Même procédure autant que vous voulez.
 Calculons le rapport des triangles blancs en tenant compte du résultat
obtenu ci-dessus. Calculons le rapport des triangles blancs en tenant compte du résultat
obtenu ci-dessus.
 Première étape: 75%
de triangles blancs; Première étape: 75%
de triangles blancs;
 Deuxième étape: 75% de triangles blancs dans les 75 % de triangles
blancs, soit 75% x 75% = 56,25%.
(ou ¾ x ¾ = 9/16). Deuxième étape: 75% de triangles blancs dans les 75 % de triangles
blancs, soit 75% x 75% = 56,25%.
(ou ¾ x ¾ = 9/16).
 Troisième étape: ¾ x ¾ x ¾ = (3/4)3 = 42,1875%. Troisième étape: ¾ x ¾ x ¾ = (3/4)3 = 42,1875%.
 Nième étape: (3/4)n . La fraction
étant inférieure à un, la puissance décroit à chaque itération pour tendre
vers 0% à l'infini. Nième étape: (3/4)n . La fraction
étant inférieure à un, la puissance décroit à chaque itération pour tendre
vers 0% à l'infini.
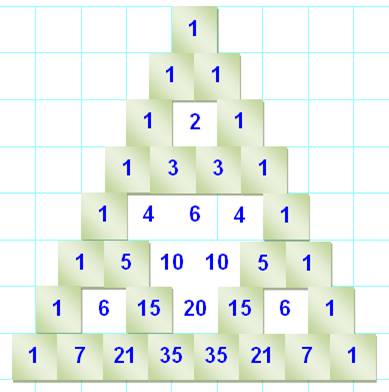
Plus le triangle
de Pascal est grand et
plus il y a de
nombres pairs.
|
![]()