|
|||||||||||||||||||||||||||||||||||
![]()
|
FONCTION
LOGIQUE "IMPLICATION" Exemples développés. Toutes les possibilités de déduction à partir de deux
propositions et de leur implication. |
|
|
||
|
Proposions: P & Q |
Assertion (implication): |
|
|
P: il
pleut. Q: le sol
est mouillé. |
S'il pleut, le sol est mouillé. |
|
|
P: les
nombres terminés par 0. Q: les
nombre multiples de 5. |
Tous les nombres terminés par 0 sont des multiples de 5. |
|
|
P: la
lampe est allumée Q:
l'interrupteur est fermé |
La lampe est allumée, alors l'interrupteur est fermé >>> |
|
|
P: il y a
un zerg Q: i y a un blob |
S'il y a un zerg, alors il y a un blob |
|
Zergs et Blobs sont des personnages de
fiction; notamment, StarCraft, jeu vidéo de 1998
Merci à Florian D. qui a
proposé ces noms et l'idée de cette page

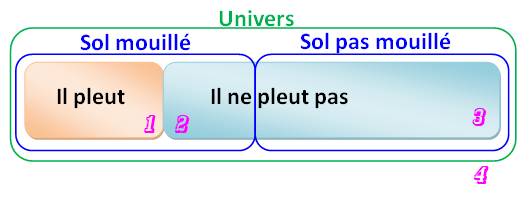
Il pleut => Le sol est
mouillé
Un ZERG => Un BLOB
|
1)
Il pleut, le sol est mouillé; or, il pleut |
|
|
|
S'il
pleut, le sol est mouillé. Or, il
pleut. Alors, le
sol est mouillé. Tous les
nombres terminés par 0 sont des multiples de 5. Or, ce
nombre est terminé par 0. Alors, il
est multiple de 5. La lampe
est allumée, alors l'interrupteur est fermé. Or la
lampe est allumée. Alors
l'interrupteur est fermé. S'il y a
un zerg, alors il y a un blob. Or, il y
a un zerg. Alors, il
y a un blob. |
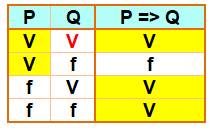
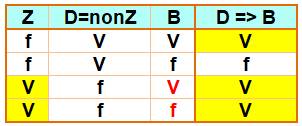
Table de vérité de l'implication
Si P => Q est vraie (jaune) et que P est vraie (jaune), alors Q est
vraie (seule ligne avec deux cases jaunes) |
|
|
2)
Il pleut, le sol est mouillé; or, il ne pleut pas |
|
|
|
S'il
pleut, le sol est mouillé. Or, il ne
pleut pas. Alors, le
sol est mouillé ou sec. Tous les
nombres terminés par 0 sont des multiples de 5. Or, ce
nombre n'est pas terminé par 0. Alors, il
est multiple de 5 ou pas. La lampe
est allumée, alors l'interrupteur est fermé. Or la
lampe est éteinte. Alors
l'interrupteur est fermé ou pas. S'il y a
un zerg, alors il y a un blob. Or, il
n'y a pas de zerg. Alors, il
y a un blob ou pas. |
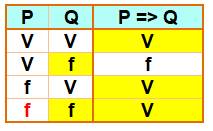
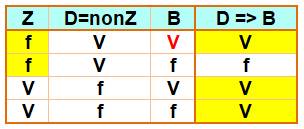
Table de vérité de l'implication
Si P => Q est vraie et que P
est fausse alors Q est vraie ou fausse (deux lignes avec deux cases jaunes) |
|
|
3)
Il pleut, le sol est mouillé; or, le sol est mouillé |
|
|
|
S'il
pleut, le sol est mouillé. Or, le
sol est mouillé. Alors, il
a plut ou pas. Tous les
nombres terminés par 0 sont des multiples de 5. Or, ce
nombre est multiple de 5. Alors, il
est terminé par 0 ou pas. La lampe
est allumée, alors l'interrupteur est fermé. Or,
l'interrupteur est fermé. Alors la
lampe est allumée ou pas. S'il y a
un zerg, alors il y a un blob. Or, il y
a un blob. Alors, il
y a un zerg ou pas. |
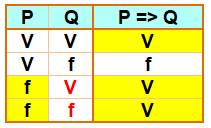
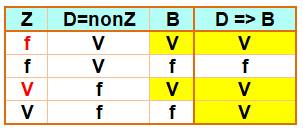
Table de vérité de l'implication
Si P => Q est vraie et que Q est vraie, alors P est vraie ou
fausse. |
|
|
4)
Il pleut, le sol est mouillé; or, le sol n'est pas mouillé |
|
|
|
S'il
pleut, le sol est mouillé. Or, le
sol n'est pas mouillé. Alors, il
n' pas plut. Tous les
nombres terminés par 0 sont des multiples de 5. Or, ce
nombre n'est pas multiple de 5. Alors, il
n'est pas terminé par 0. La lampe
est allumée, alors l'interrupteur est fermé. Or,
l'interrupteur n'est pas fermé. Alors la
lampe est éteinte. S'il y a
un zerg, alors il y a un blob. Or, il
n'y a pas de blob. Alors, il
n'y a pas de zerg. |
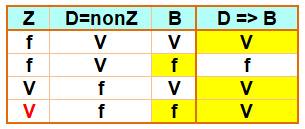
Table de vérité de l'implication
Si P => Q est vraie et que Q est fausse, alors P est fausse. |
|
Un ZERG => Pas de BLOB
|
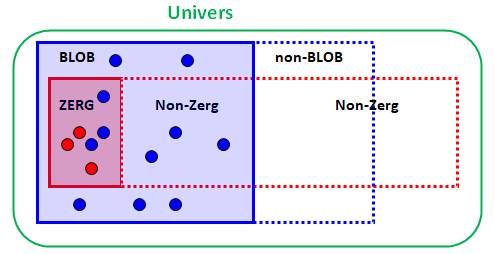
5)
Un zerg => pas de blob; or, il y a un zerg |
|
|
|
Dans cet univers S'il
pleut, le sol n'est pas mouillé serait une phrase vraie. La pluie, sitôt au
sol, disparaitrait … Tous les
nombres terminés par 0 ne seraient pas des multiples de 5. La lampe est
allumée, alors que l'interrupteur est ouvert. Ces trois
cas étant utopiques et, pour ne pas introduire de la confusion, ils ne sont
plus commentés. Exemple suivi S'il y a
un zerg, alors il n'y a pas de
blob. Or, il y
a un zerg. Alors, il
n'y a pas de blob Voir le diagramme ci-dessous. |
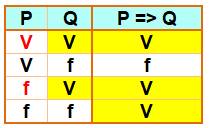
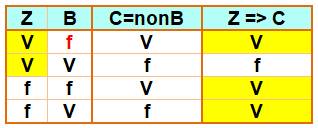
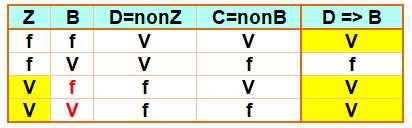
Table de vérité de l'implication Z = il y a un zerg B = il y a un blob. C= il n'y a pas de blob.
La table de vérité de
l'implication s'applique à Z et C Cette implication est vraie (jaune). Il ya un zerg (première colonne V jaune) Il n'y a pas de blob (la première ligne est jaune). |
|
|
6)
Un zerg => pas de blob; or, il n'y a pas de zerg |
|
|
|
S'il y a
un zerg, alors il n'y a pas de
blob. Or, il
n'y a pas de zerg. Alors, il
y a un blob ou pas. |
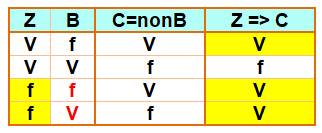
Table de vérité de l'implication
Indécision. |
|
|
7)
Un zerg => pas de blob; or, il y a un blob |
|
|
|
S'il y a
un zerg, alors il n'y a pas de
blob. Or, il y
a un blob. Alors, il
n'y a pas de zerg. |
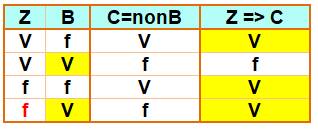
Table de vérité de l'implication
Il n'y a pas de zerg. |
|
|
8)
Un zerg => pas de blob; or, il n'y a pas de blob |
|
|
|
S'il y a
un zerg, alors il n'y a pas de
blob. Or, il
n'y a pas de blob. Alors, il
y a un zerg ou pas. |
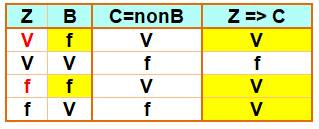
Table de vérité de l'implication
Indécision. |
|
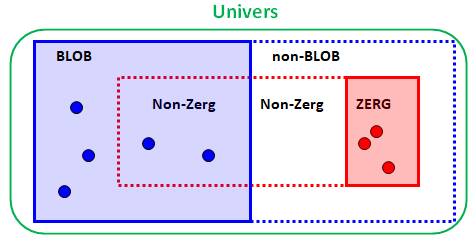
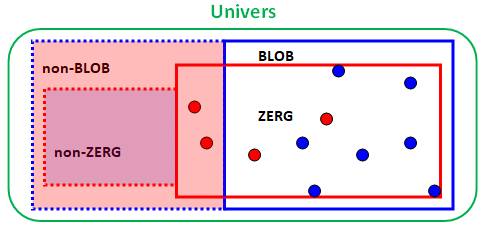
Pas de ZERG => Un BLOB
|
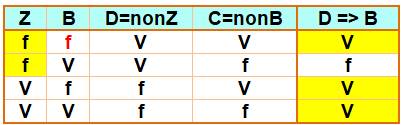
9)
Pas de zerg => un blob; or, il y a
un zerg |
|
|
|
S'il n'y
a pas de zerg, alors il a un blob. Or, il y
a un zerg. Alors, il
y a un blob ou pas. |
Table de vérité de l'implication
Les trois colonnes de droite reflètent bien la table de vérité de
l'implication. Il est vrai qu'il y a un zerg. Impossible de conclure pour les blobs (rouge). |
|
|
10)
Pas de zerg => un blob; or, il n'y
a pas de zerg |
|
|
|
S'il n'y
a pas de zerg, alors il a un blob. Or, il
n'y a pas de zerg. Alors, il
y a un blob. |
Table de vérité de l'implication
Dans ce cas, il a un blob. |
|
|
11)
Pas de zerg => un blob; or, il y a
un blob |
|
|
|
S'il n'y
a pas de zerg, alors il a un blob. Or, il y
a un blob. Alors, il
y a un zerg ou pas. |
Table de vérité de l'implication
Indécision. |
|
|
12)
Pas de zerg => un blob; or, il n'y
a pas de blob |
|
|
|
S'il n'y
a pas de zerg, alors il a un blob. Or, il
n'y a pas de blob. Alors, il
y a un zerg. |
Table de vérité de l'implication
Il est vrai qu'il y a un zerg |
|
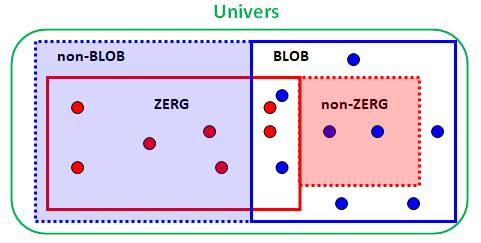
Pas de ZERG => Pas de BLOB
|
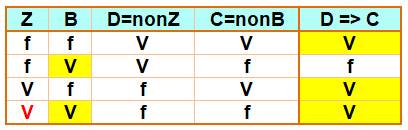
13)
Pas de zerg => pas de blob; or, il
y a un zerg |
|
|
|
S'il n'y
a pas de zerg, alors il n'y a pas de blob. Or, il y
a un zerg. Alors, il
y a un blob ou pas. |
Table de vérité de l'implication
Les trois colonnes de droite reflètent bien la table de vérité de
l'implication. Il ya un zerg. Indécision pour les blobs. |
|
|
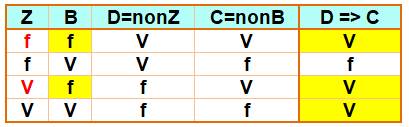
14)
Pas de zerg => pas de blob; or, il n'y
a pas de zerg |
|
|
|
S'il n'y
a pas de zerg, alors il n'y a pas de blob blob. Or, il
n'y a pas de zerg. Alors, il
n'y a pas de blob non plus. |
Table de vérité de l'implication
Les trois colonnes de droite reflètent bien la table de vérité de
l'implication. Il y a un zerg. Indécision pour les blobs |
|
|
15)
Pas de zerg => pas de blob; or, il
y a un blob |
|
|
|
S'il n'y
a pas de zerg, alors il n'y a pas de blob blob. Or, il y
a un blob. Alors, il
y a un zerg. |
Table de vérité de l'implication
Il y a un zerg. |
|
|
16)
Pas de zerg => pas de blob; or, il
n'y a pas de blob |
|
|
|
S'il n'y
a pas de zerg, alors il n'y a pas de blob blob. Or, il
n'y a ps de blob. Alors, il
y a un zerg ou pas. |
Table de vérité de l'implication
Indécision |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()