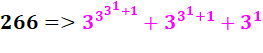|
Édition du: 15/03/2024 |
|
INDEX |
Types de Nombres – Motifs |
||
Faites un double-clic pour un retour en haut de page
![]()
|
BASES HÉRÉDITAIRES ou itérées SUITES de GOODSTEIN Où il question
de factoriser tous les exposants de la factorisation d'un nombre. |
||
|
|
Sommaire de cette page >>> Notation héréditaire en base n >>> Dilatation >>> Suite de Goodstein |
Débutants Glossaire |
Reuben Goodstein
(1912-1985)
|
Mathématicien
et logicien britannique. Université
de Leicester. Son
théorème est un théorème parmi les premiers qui sont indémontrables dans l'arithmétique de
Peano. |
Voir Contemporains
|
Numération Notre numération
décimale consiste à écrire des chiffres dans une position qui leur
confère un poids en puissance de 10, on dit que la numération est effectuée
en base 10. Il est toujours possible une autre
base, notamment la base 2 pour écrire les nombres en binaire. |
Écriture d'un nombre en base n
Exemple en base 10 |
|
|
Notation héréditaire ou itérée Elle consiste à appliquer la numération des
nombres aux exposants eux-mêmes, et même aux exposants d'exposants, etc. Tous les nombres sont exprimés dans la base
choisie, y compris les exposants. Résultat: aucun nombre ne doit être plus grand
que la base. Comme pour l'écriture normale, l'écriture héréditaire
est unique. |
Écriture en base 2
Écriture en base 2 héréditaire
Écriture en base 3 héréditaire
|
|
|
Dilatation À partir d'un nombre écrit en base héréditaire, le
procédé de dilatation consiste à remplacer toutes les bases par la base +1. Ce procédé est utilisé pour construire les suites
de Goodstein, suites qui font "voler" les nombres vers de grandes
altitudes avant de redescendre inéluctablement vers zéro. |
Exemple Après dilatation, le nombre 266 devient:
Ce nombre comporte 38 chiffres en base 10. Un
nombre dilaté est souvent très dilaté. Ce nombre dilaté en base 4 passe à 616 chiffres
en base 4. |
|
|
Définition Il s'agit d'une suite attachée à un nombre m
donné, notée G(m). D'abord m est exprimé en base 2 héréditaire. La base en cours est remplacée par la base + 1 (dilatation) et le résultat est diminué
de 1. Poursuivre jusqu'à atteindre 0. Lors du remplacement par la base suivante,
parfois un calcul est nécessaire pour s'assurer que tous les nombres sont
inférieurs à la valeur de la base. Théorème (1944) Quelle que soit la valeur de m, la suite de
Goodstein se termine toujours par 0. Parfois, les valeurs intermédiaires sont
incroyablement élevées. Pour m = 4, c'est les cas. On monte jusqu'à des
exposants en quatre cent millions ! Pourquoi le moins 1 ? C'est cette décrémentation qui rogne doucement
les grands nombres et qui fait décroitre la suite vers 0. Intérêt Ces suites et le théorème sont utilisés
essentiellement en mathématiques théoriques: construction de fonctions
calculables, informatique théorique. Ce théorème ne pas se démontrer par récurrence,
c'est-à dire en ne nous servant que des entiers et des autres opérations.
L'envol est tel que la suite prendre des valeurs tellement grandes qu'elle
dépasse n'importe quelle fonction dont on peut démontrer l'existence par
récurrence. Pour plus d'explications voir
l'article de Patrick Dehornoy |
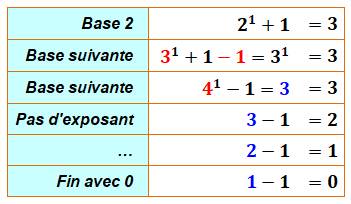
Exemple pour m = 3
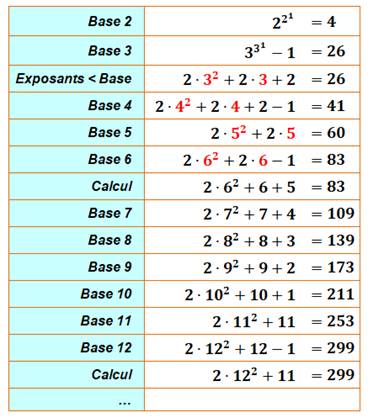
Exemple pour m = 4
La quantité d'itérations
pour atteindre 0 est un nombre avec environ 130 millions de chiffres. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Numerati/aaaBASE/Heredita.htm
|