|
|||||||||||||||||||||||||||||||||
![]()
|
QUARTILES & QUANTILES La population est divisée en
quatre groupes d'individus ou dix groupes ou
cent groupes ou n groupes. Quels sont les individus
représentatifs de chaque sous-groupe? Différents types de calculs
… |
|
|
|
|
En bref, le quartile est la médiane de chaque demi-groupe.
Les quartiles les
séparent en quatre groupes. Les déciles en 10 Les centiles en 100. Les quantiles en n.
|
|
Définition comme dans les
livres
|
Quartiles: réels qui caractérisent l'étendue des
valeurs prises par un caractère
quantitatif X. Premier quartile (Q1): valeur du caractère X
telle que:
Calcul: lorsque plusieurs valeurs son
possibles, on prend la valeur de la demi-somme entre les valeurs possibles
extrêmes |
D'après Dictionnaire des
mathématiques – Bouvier, George et Le Lionnais
|
|
|
|
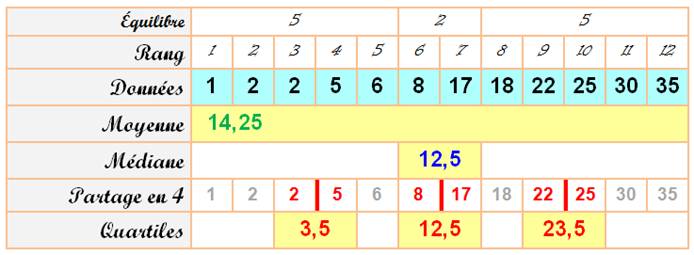
Dans tous les cas, les données sont ordonnées par
valeurs croissantes. La méthode consiste à diviser la quantité par 4 et,
comme pour la médiane, si la coupure tombe entre deux valeurs, faire la demi-somme (moyenne) de ces valeurs. Chaque
quartile compte 12 / 4 = 3 individus.
Q1
= 3,5; Q2 = médiane = 12,5; et, Q3 = 23,5 Intervalle interquartile: [3,5; 23,5]: la moitié des individus (6)
ont une valeur comprise entre 3,5 et 23,5. Écart interquartile: 23,5 – 3,5 = 20. Remarque
sur deux méthodes alternatives simples, mais peu précises Pour simplifier, une alternative consiste à
prendre les valeurs en limite de
bordure. (Ici: Q1 = 2, et Q3 = 22). Cette alternative présente deux
inconvénients:
Une autre méthode consiste à prendre
l'arrondi à la valeur entière la plus proche de 0,25 pour Q1 et 0,75 pour Q3
de la quantité de valeurs plus une. Mêmes remarques que ci-dessus. (ici, nous
aurions: rang 1 = 0,25 x 13 = 3,25 arrondi à 3 et Q1 = 2; tandis que le rang
3 = 0,75 x 13 = 9,75 arrondi à 10 et Q3 = 25.
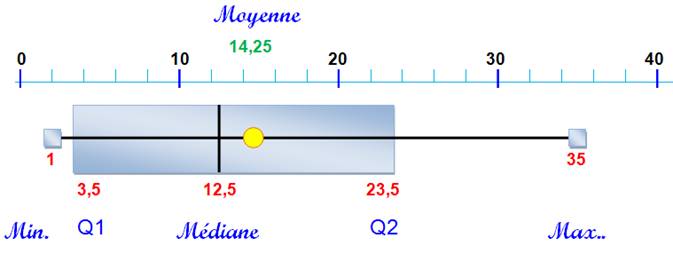
Représentation
par un diagramme en boite En
horizontal, toutes les valeurs croissantes prises par la population. Les
cinq points remarquables (rouge) et la moyenne (vert) sont notés comme
indiqué:
|
|
|
|
|
|
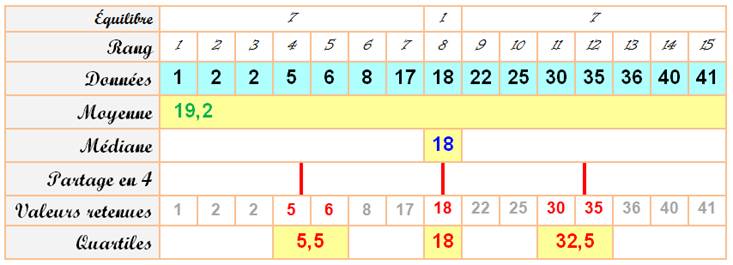
En
divisant 15 par 4, on obtient 3,75 et l'entier supérieur est: 4
Q1
= 5,5 ; Q2 = médiane = 18 et Q3 = 32,5. Intervalle interquartile: [5,5; 32,5]: la moitié des individus
(15/2 arrondi à 7) ont une valeur comprise entre 5,5 et 32,5. Écart interquartile: 32,5 – 5,5 = 27. Remarque Pour simplifier, une alternative consiste à
prendre les valeurs arrondies supérieures de la division. Pour Q1, nous
aurions: 15/4 = 3,75 arrondi à 4 et la quatrième valeur donnerait Q1 = 5. De
même, au rang 15 x 3/4 = 11, 25 arrondi à 12 donnerait Q3 = 35. |
|
|
|
|
|
Les programmes sur machines (calculettes, ordinateurs)
calculent des quartiles sensiblement différents. Nous avons calculé la
demi-somme des valeurs encadrant la frontière des quarts. Ces programmes font
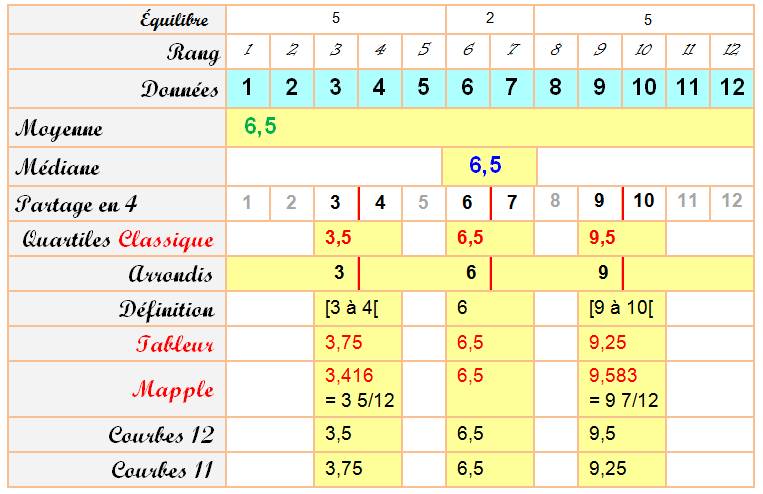
des calculs plus sophistiqués Exemple avec la série
toute simple des 12 nombres entiers consécutifs:
Quartiles classiques: calcul par demi-somme autour de la
frontière. Recommandé. Quartiles arrondis: calcul par le rang arrondi à l'entier
supérieur. Parfois utilisés, mais ce
calcul présente des inconvénients clairement visibles sur ce tableau. Quartiles définition: fourchette répondant à la définition
des quartiles. Quartiles tableur: donné par la fonction quartile d'Excel. Quartiles Maple: donné par la fonction quartile du
logiciel de calcul Maple. Quartiles Coubes 12: lecture de la valeur sur le graphique
montrant la série de valeurs, en divisant par 12 (comme 12 valeurs). Proche de Maple. Quartiles Coubes 11: lecture de la valeur sur le graphique en
divisant par 11 (comme 11 intervalles). Ce
que donne le Tableur. Dans tous les cas (hors méthode de
l'arrondi), les valeurs se trouvent dans la fourchette donnée par la
définition. |
|
|
La notion de quartile est
extensible aux déciles ou aux centiles pour une division de la population en
dix ou cent sous-groupes de même nombre d'individus. Elle est généralisable à
une division par un nombre quelconque: quantiles. Le calcul manuel devient vite fastidieux. Les programmes de
calcul mathématiques prennent
avantageusement la relève. |
|
The quartiles of a set of values are the three points that divide the data set into four
equal groups, each representing a fourth of the population being sampled. A
quartile is a type of quantile. First quartile (Q1) or lower
quartile or 25th percentile. Second quartile (Q2) or median or 50th percentile. Third quartile (Q3) or upper
quartile or 75th percentile. The difference between
the upper and lower quartiles is called the interquartile
range. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Probabil/Quartile.htm |
![]()