|
|||||||||||||||||||||||||||||
![]()
|
Les statistiques le démontrent: il
meurt plus de gens dans leur lit qu'au front. L'Ombre du vent – Carlos Ruiz
Zafon |
|
Brièvement, et
dans sa forme la plus concrète, l'objet des méthodes statistiques est la
réduction de données. Une quantité de données qui, en général, de par sa
simple masse est incapable d'entrer en l'esprit, doit être remplacée par des
quantités en nombre relativement faible et qui doivent représenter
adéquatement le tout ou qui, en d'autres termes, doivent contenir le plus
possible - idéalement la totalité - de l'information pertinente contenue dans
les données originelles. Ronald
Fisher – 1922 |
Voir
Pensées & humour
|
|
||
|
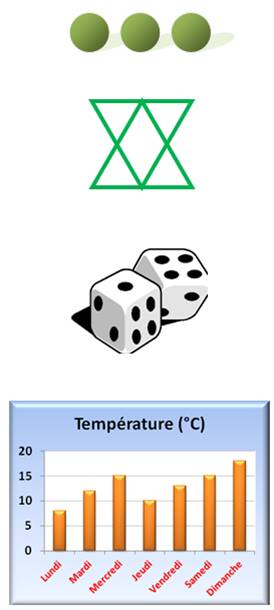
Quatre
manières d'apprécier une quantité: Je compte 3
pions verts sur ce dessin. Je dénombre
sur cette figure 2
grands triangles, Je prédis: probabilités Si
je lance un dé de nombreuses fois, je tomberai une fois sur six sur le 1 (ou
le 2, etc.). J'étudie: statistiques Quelle
a été la température maximale de la semaine? (18°C); la plus fréquente?
(15°C); la température moyenne? 13°C; etc. |
|
|
|
|
||
|
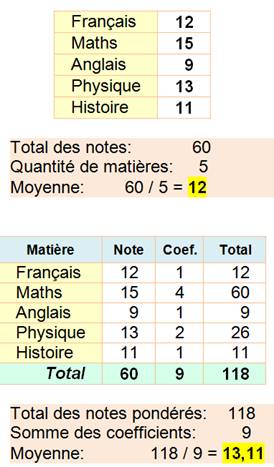
Pratiquement tous les manuels
prennent pour exemple les notes en classe. Nous allons faire de même. La liste de mes notes en classe est
appelée une série numérique. Tout de suite, on a envie de
calculer la moyenne. Mais le prof vous annonce qu'il y a
des matières qui comptent plus que les autres: les maths comptent quadruple,
et la physique compte double. Chaque note doit être pondérée par
un coefficient multiplicatif. Alors, on calcule la nouvelle
moyenne, dite moyenne pondérée. |
|
|
|
Énigme 1 La moyenne des âges
d'Adam et Baptiste est 12 et celle de Baptiste et Chloé est 10 alors que leur
différence d'âge est de 2 ans. Quel est l'âge de
chacun ? |
Solution
(équations) (A + B) / 2 = 12 ; (B
+ C) / 2 = 10 ; B = C + 2 C + 2 + C = 20 => C
= 9 B = C + 2 = 11 A = 24 – B = 13 Solution
(raisonnement) On essaie la moyenne
12 avec 13 et 11, puis la moyenne 10 avec 11 et 9. Bingo, on a bien 11 = 9 +
2 |
|
Énigme 2 La moyenne des âges
d'Adam et Chloé, l'ainée des sœurs, est 16 et celle des sœurs est 10 alors
que la différence d'âge entre l'ainée et sa cadette est de 2 ans. Combien de sœurs au
minimum, et âges en nombres entiers de chacun ? |
Solution
avec 2 sœurs (A + B) / 2 = 16 ; (B
+ C) / 2 = 10 ; B = C + 3 A = 41/2, B = 23/2, C
= 17/2 Seule possibilité pour
obtenir des âges entiers, il existe une troisième sœur. Cette sœur a un âge
impair indéterminé entre 1 et 25 ans, par exemple: A = 16; B = 16, C = 13
et D = 1 La famille pourrait
aussi comprendre 5 sœurs: A = 10, B = 22, C= 19,
D = 5, E = 3 et F = 1 |
Voir Énigmes de familles
|
|
||
|
Une représentation graphique sera
une bonne manière de se rendre compte des notes, de les visualiser, de les
comparer. Pour cela, il est plus commode de
les classer par ordre croissant (ou décroissant). Un dessin avec des barres dont la
hauteur représente chaque note semble approprié. Ce diagramme qui, en quelque sorte,
raconte l'histoire de mes notes, est un histogramme. Il permet de mieux apprécier l'étendue de mes notes; je peux voir si mes
notes sont très dispersées ou pas. |
|
|
|
|
||
|
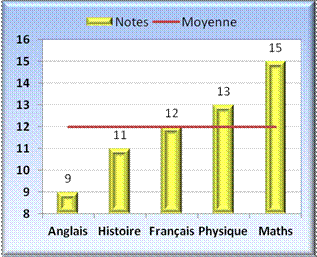
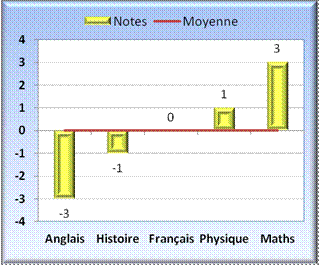
Vous conviendrez qu'un graphique
dont l'échelle va de 0 à 20 pour représenter une étendue de 6, c'est de la
place perdue; nous avons envie de nous concentrer sur la zone où se trouvent
les notes. Une bonne idée consiste à prendre la
moyenne comme référence et d'observer toutes les notes par rapport à cette
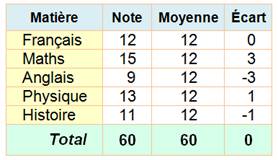
moyenne, en plus ou en moins. Nous pouvons poursuivre nos
investigations en donnant l'écart de
chaque note par rapport à la moyenne. Remarquez que la somme algébriques
(les plus et les moins) des écarts est nulle. En reprenant les écarts comme
valeurs dans notre graphique nous obtenons un histogramme
centré sur la moyenne. Il s'agit du même histogramme, sauf
que nous avons fait glisser toutes les notes de 12 points vers le bas. |
|
|
|
|
||
|
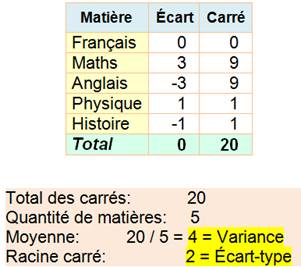
Une telle dispersion des notes de -3
à +3, comment la caractériser? La
moyenne donnerait zéro: pas un
bon plan! Nous pourrions faire la moyenne des
valeurs absolues. Oui! En fait, mieux, prenons le carré qui
sera toujours positif. La moyenne des carrés des écarts
s'appelle la variance et sa racine carrée,
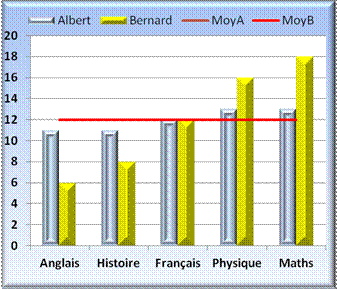
l'écart-type. Deux personnes peuvent avoir à peu
près la même moyenne mais avec des écarts
très différents. L'un (Albert) peut avoir ses notes
toutes autour de 12 et l'autre (Bernard) des notes allant de 6 à 18, par
exemple. La variance (ou l'écart-type)
témoignent de cette dispersion. Note: on obtient facilement ces valeurs avec les
fonctions statistiques des tableurs; pour la variance choisir la variance-
population (Var-P). |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()