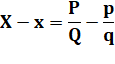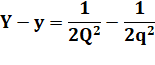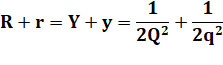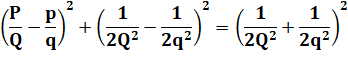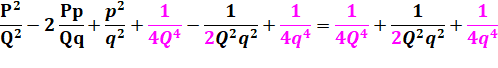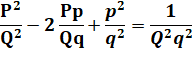|
|||||||||||||||||||||||||||||||||||
![]()
|
Suites de FAREY et Cercle de Ford |
|
Lester
Ford
(1886-1967), mathématicien américain. John Faret (1766-1826),
géologue anglais. |
Une idée
des cercles de Ford
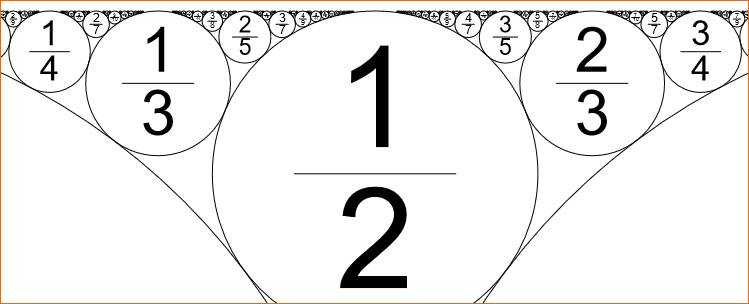
Source
image: Ford Circle
Exemple
de ces fractions
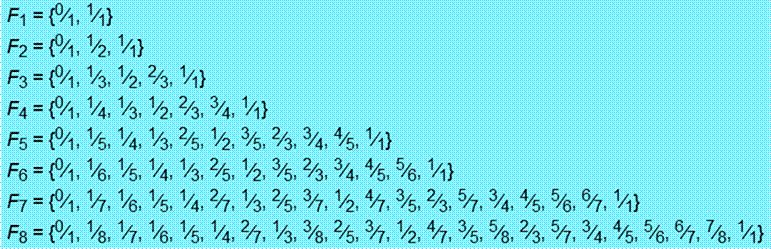
|
|
|||||||||||
|
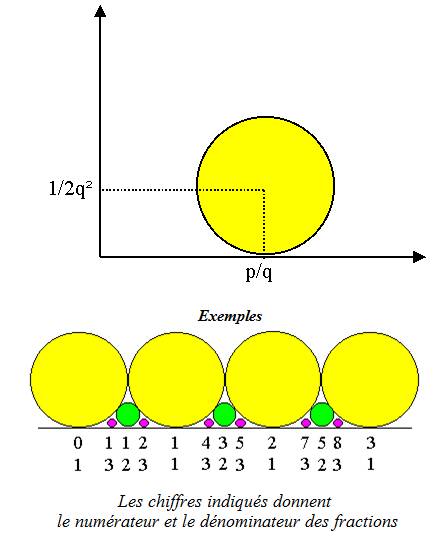
Principe du tracé Avec les fractions de Farey, on peut obtenir une figure bien étrange,
symétrique et de caractère fractal. On dessine les cercles de
caractéristiques suivantes => |
|
||||||||||
|
Cercles de Lester R. Ford (1938) |
|||||||||||
|
Propriétés |
Les cercles ne se coupent jamais. Ils sont tangents les
uns à d'autres. Ceci s'explique par la propriété: a/c, b/d et nouvelle
fraction intermédiaire (a+b) / (c+d). En augmentant l'ordre de la suite de
Farey d'autres cercles s'intercalent ceci, jusqu'à l'infini. Les points de tangence représentent
toutes les fractions possibles, soit tous les nombres rationnels. |
||||||||||
|
Note |
Quand on pense que ces points de
tangence, en nombre infini, ne couvrent pas tous les points de la droite. Il
y encore de l'espace pour une infinité
de nombres irrationnels dans les
interstices. Chaque cercle est tangent à une infinité de cercles. |
||||||||||
|
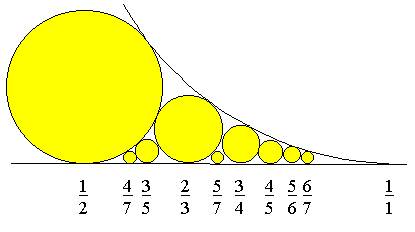
Illustration Ordre 7 de 1/2 à 1 |
|
||||||||||
|
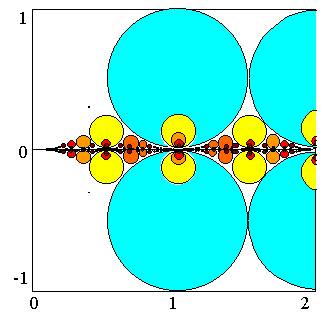
Vue artistique avec tracé du symétrique vers le bas |
|
||||||||||
|
|
|||
|
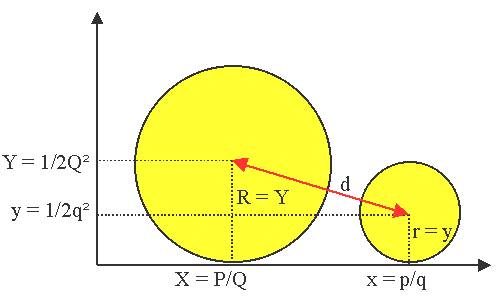
Soit deux fractions de Farey p/q et P/Q |
|
||
|
Si les deux cercles sont de
Farey/Ford, ils sont tangents. On suppose qu'ils sont tangents et
on montre que les deux fractions sont deux fractions successives de
Farey. |
|||
|
Horizontal |
|
||
|
Vertical |
|
||
|
Oblique (R + r) |
|
||
|
Pythagore |
|
||
|
Calculs |
|
||
|
|
|||
|
|
|||
|
Bilan |
|
||
|
Cercle de Farey |
On
retrouve la propriété des fractions
successives de Farey |
||
Merci à Vincent Lesbros
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()