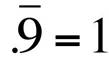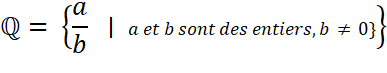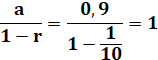|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES
RATIONNELS
|
Voir Nombres périodiques / Valeur de
Pi (22/7)
|
1608 - Notation à virgule des nombres décimaux
introduite par Willebrord Snellius ou
Willebrord Snell Van Royen (NL), le même que celui de la loi de Snell- Descartes sur la réfraction. |
|
Occasion
de pratiquer un féroce faux-amis en anglais: A number is rational if and
only if its decimal digits are eventually periodic. Eventually veut dire:
finalement ultimement. |
|
|
|
|
Nombres
rationnels ou nombres fractionnaires Vient de quotiente (Peano) Il existe des nombres à virgule en plus de
ceux qui servent à mesurer (Ex: 1,2 cm, 3,25 l, 10,5 kg …). Ce sont ceux
formés avec des fractions telles que 1/3, 1/7, 12/13 ... Les chiffres
derrière la virgule ne s'arrêtent jamais. Un motif se
répète sans cesse. Ces
nombres à fraction (à ration !) sont appelé rationnels. Exemples: 1/3 =
0,333… 1/7 = 0,142857 142857 … Ils
forment l'ensemble des nombres rationnels noté Cet
ensemble possède les propriétés d'un corps. L'ensemble des nombres entiers relatifs ( Les nombres entiers peuvent aussi se mettre sous la forme d'une
fraction, avec un dénominateur à 1. Ex: 2 = 2/1, 11 = 11/1 … Le
développement décimal des
fractions peut être limité (1/2 = 0,5) ou périodique (1/3 = 0,333). Exemples: 3,5 = 7/2 2 = 2/1 0,123 = 123/1000 0,333… = 1/3 Rational Numbers: the numbers you can make by dividing one integer by another (but not
dividing by zero). In other words fractions. Q is for
"quotient" (because R is used for the set of real numbers). Examples: 10/5 = 2 7/2 = 3.5 - 256/100 = -2.56 |
|
|
|
|||||||||||||
|
Opérations
sur les entiers
Opérations sur les ENTIERS =>
Nombres RATIONNELS Voir Nécessité des différents types de nombres Nombres
rationnels
composent, avec le nombre 0, l'ensemble des nombres rationnels.
Qui se lit: L'ensemble des
nombres rationnels (Q) est l'ensemble des fractions (a/b) pour lesquelles a
et b sont des nombres entiers, positifs ou négatifs, sachant que b ne peut
pas prendre la valeur zéro. |
|||||||||||||
|
|
|
|
avec des nombres
rationnels produisent des nombres rationnels.
son
développement décimal1 est périodique2. 1 décimal
ou toute autre base. 2
périodique à partir d'un certain rang.
0,25 25 26 25 0,111121111 0,123 123 124 123
|
|
Voir Nombres
Périodiques
|
Rationnel à partir
d'irrationnels |
|
|||||||||||||||||||||||||||
|
Racine de deux puissance racine de deux
tout cela à la puissance racine de deux vaut deux.
La solution est quasiment dans le constat
précédent. Notez qu'avec la démonstration fournie, on
ne connait pas la nature de |
Trois
nombres irrationnels donnent un rationnel:
En effet
Voir Puissances
à étage Deux
nombres irrationnels donnent un rationnel: Considérons Soit N est rationnel
et le problème est résolu. Sinon, et c'est
le seul cas possible, N est irrationnel. Dans ce cas élevons N à la
puissance racine de deux: Que N soit
rationnel ou non, nous avons bien deux nombres irrationnels dont l'un à la
puissance de l'autre donne un nombre rationnel. |
|||||||||||||||||||||||||||
|
English: Let |
||||||||||||||||||||||||||||
|
Table
pour les racines à étages, et cas où le résultat est rationnel (entier) en jaune. Voir
calculs en racines à étages |
Table de
1 à 12
|
|||||||||||||||||||||||||||
Anglais: Irrational
to an irrational power can be rational
Voir Racine de deux / Nombre deux / Reconnaître les irrationnels
|
associée à un NOMBRE PÉRIODIQUE |
|
|
Exemple 0,25
25 25… =
0,25 x 1,010101… =
0,25 (1 + 10-2 + 10-4 + 10-6 +…) =
0,25 (1 / (1 – 10-2 ) =
0,25 (1 / (1 – 0,01 ) =
0,25 (1 / 0,99) =
(25 / 100) (1 / 0,99) =
25 / 99 Voir aussi en Nombres
périodiques Rappel
sur la somme d'une série géométrique 1
+ a + a² + a3 + … + an = 1 / (1 – a) que
l'on peut vérifier facilement en développant: (1 – a) (1 + a + a² + a3 + … + an)
= 1 – an+1 Autres
exemples 25 / 99 = 0,252525… 25 / 999 = 0,250 250 250… 123 / 999 = 0,123 123 123… 123456789
/ 999999999 = 0,123456789 123456789 … 123456789
/ 555555555 = 0,2222222204 222222204
… 123456789
/ 111111111 = 1,111111102 111111102… 123456789
/ 1111111111 = 0,111111110 1111111110… 123456789
/ 1111111101 = 0,111111111111111111111111111111 Note (avec le même mode de calcul que ci-dessus): 0,999…
= 0,9 x 1, 111… = 0,9 (1/0,9) = 1 Il
y a bien égalité car entre 0,999 … et 1, il n'existe aucun espace pour un
nouveau nombre. >>> En
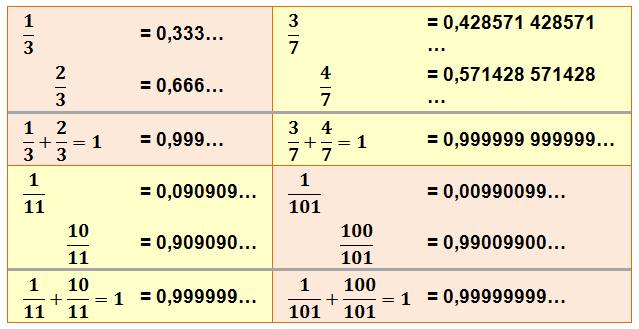
fait 0,111…
= 1/9 0,222…
= 2/9 0,333…
= 3/9 = 1/3 0,444…
= 4/9 0,555…
= 5/9 0,666…
= 6/9 = 2/3 0,777…
= 7/9 0,888…
= 8/9 0,999…
= 9/9 = 3/3 = 1 Voir Repdigit
/ Nombre
0,999 / Nombres périodiques / Nombre 1/100 / Nombres décimaux en xxx, 999 |
|
|
|
||
|
Cette
égalité semble étrange et difficile à admettre par certains. Pourtant, aucun
doute chez les mathématiciens et plusieurs démonstrations le prouvent. |
Le
nombre 0,999… est un nombre décimal périodique,
noté Cette
égalité n'est pas un cas unique. Tout nombre rationel
peut s'écrire avec une infinité de 9. Exemples: 2
= 1,999… 2,5
= 2,4999… 12345,678
= 12345,677999… |
|
|
Propriété des nombres Si 2
nombres réels sont différents, alors il en existe au moins un 3e
entre les deux, différent des deux autres. |
Or, on ne
peut pas intercaler de nombre
entre 0, 999 ... et 1. Ils sont donc égaux. |
|
Prenons l'égalité suivante Multiplions par 3 |
1/3 1 |
= = |
0,333
… 0,999
… |
|
|
Avec les nombres
périodiques |
Soit n notre nombre Multiplions par 10 Soustraction Et, résultat |
n 10 n 9 n n |
= = = = |
0,999
… 9,999
… 9 1 |
|
Avec
le développement décimal |
On appelle M la moyenne
arithmétique entre 0,999… et 1. C'est un nombre qui se situe entre 0,999…
et 1. |
|||
|
|
Supposons Moyenne |
0,999… 0,999… |
< < |
1 M < 1 |
|
|
L'écriture décimale de M commence par : |
0,9xyz… |
= |
M |
|
|
Or |
0,99 |
< |
M |
|
|
de M commence par: |
0,99yz… |
= |
M |
|
|
Soit, en recommençant |
0,999… |
= |
M |
|
|
Or, la moyenne n'est pas égale à l'un des nombres |
L'hypothèse est fausse. |
||
|
Autre fin |
Notons |
n |
= |
0,999… |
|
|
Par définition |
M |
= |
|
|
|
Nous avons trouvé que: |
M |
= |
n |
|
|
Égalisons |
n |
= |
|
|
|
Qui amène à: |
n |
= |
1 |
|
Avec une suite
géométrique |
Développement fractionnaire |
0,999… |
= |
|
|
|
C'est une suite géométrique de
raison |
r |
= |
|
|
|
La somme vaut |
S |
= |
|
|
Avec une limite |
Différence |
1 – 0,9 1 –
0,99 1 –
0,999 1 –
0,99…9k |
= = = = |
0,1 0,01 0,001 1/ 10k |
|
|
Limite |
|
= |
0 |
|
Somme de factions pour l'amusement |
|
Voir Énigme du chocolat / Brève
638
![]()
|
Suite |
|
|
DicoNombre |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()