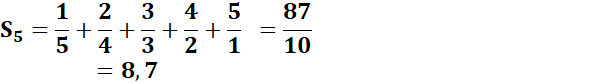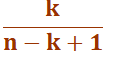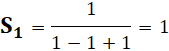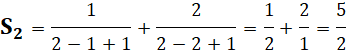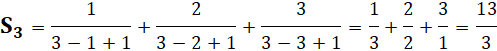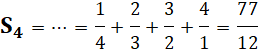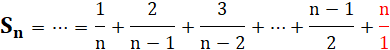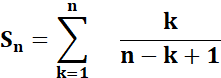|
|||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SÉRIE HARMONIQUE Pondérée Comme la série harmonique
cette série est divergente et il n'existe pas de formule donnant directement
la valeur de Sn. Cette page présente une tentative
de formulation de la somme de la série harmonique pondérée. Exemple de somme
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Premiers termes Notez que le premier terme est 1/n et le dernier n. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
Type |
Sorte de série
harmonique (somme des inverses des nombres), pondérées les nombres
décroissants. |
|||||||||||||||||||||||||||||||||||||||||||
|
La somme s'écrit |
Somme
pour k = 1 à k = n de toutes les fractions en k / (n-k+1). |
|||||||||||||||||||||||||||||||||||||||||||
|
Valeurs La série diverge très nettement. Normal le dernier terme est égal à n et le reste est positif. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||
|
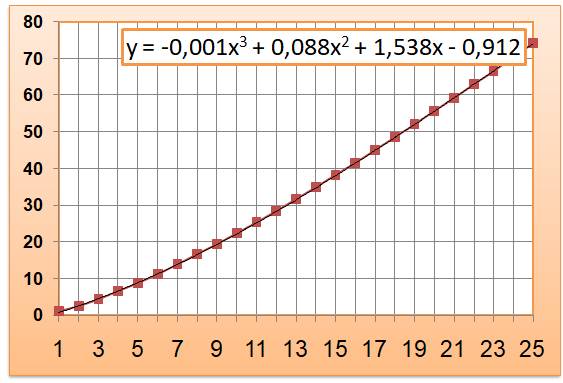
Allure de la série Sur 25 valeurs la courbe de régression du 3e degré épouse bien la
forme de la courbe. Mais, la formule déraille pour des valeurs plus grandes! |
|
||
|
Avec 100 points |
Courbe
de régression calculée par le tableur pour n de 1 à 100 S100 = -0,0001024876 x3 + 0,02736588
x² + 2,565553 x – 5,064159 Précision
relative faible jusqu'à n = 10
(>4%); elle
est inféreiyre à 1% à partir de n = 23. Pour
n = 100, S = 423,925 alors que la formule nous donne 422,660 (0,3%) La
contribution des deux premeirs termes: 171,17 et des deux derniers: 251,5.
Malgré les petits coefficients, la contribution des deux premiers termes est
importante. Cependant
pour n = 150, S = 694,3 alors que la formule nous donne 649,6, soit 6,4% de
précision relative. La formule déraille vite. S150 = -0,0000474 x3 + 0,01877 x² + 2,92 x – 8,089 Les
formules sont bien évidemment évolutives selon l'amplitude des points
utilisés |
||
|
Calcul d'une formule du deuxième
degré Cette formule calculée sur les trois premiers points ne marche pas
pour les suivants. |
S = An² + Bn + C
|
|
|
|
Calcul d'une formule du troisième
degré Cette formule calculée sur les quatre points ne marche pas pour les
autres. |
S = An3 +
Bn² + Cn + D
|
|
|
|
Calcul d'une formule du troisième
degré Avec les points n = 2, 10, 25 et 100 |
S = -0,0002030399 x3 + 0,04313408 x² + 1,972399299x – 1,615710612 Si
la précision relative est
inférieure à 0,5% en milieu deplage, elle s'envole dès que l'on dépasse 100% (voir la courbe ci-dessous). |
||
|
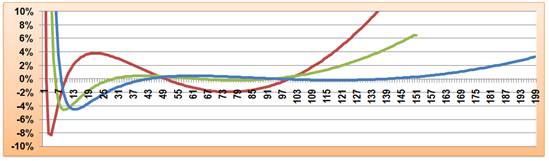
Comparaison des précisions
relatives Confirmation que la modélisation rigoureuse de la série est
impossible. |
En rouge: la courbe pour la formule du troisième degré avec
les quatre points contraints (2, 10, 25, 100). L'ondulation est forte et la
courbe s'échappe après n = 100. En vert : la courbe de régession de S100
calculée par le tableur. Elle serait plus plate et donc plus précise pour la
plage centrale. En bleu : la courbe de régession de S150
calculée par le tableur. Plus précise pour n entre 50 et 150. |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()