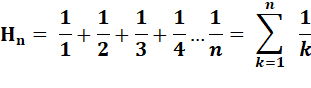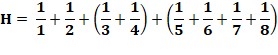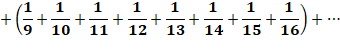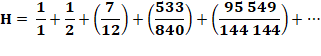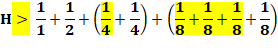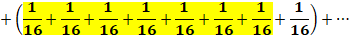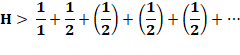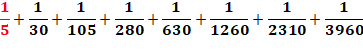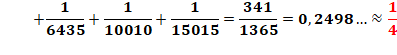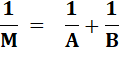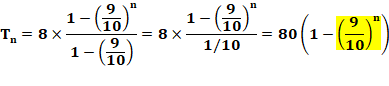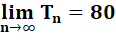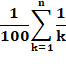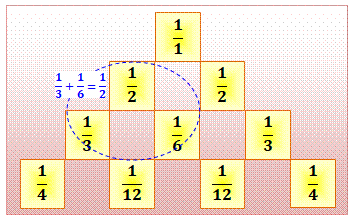
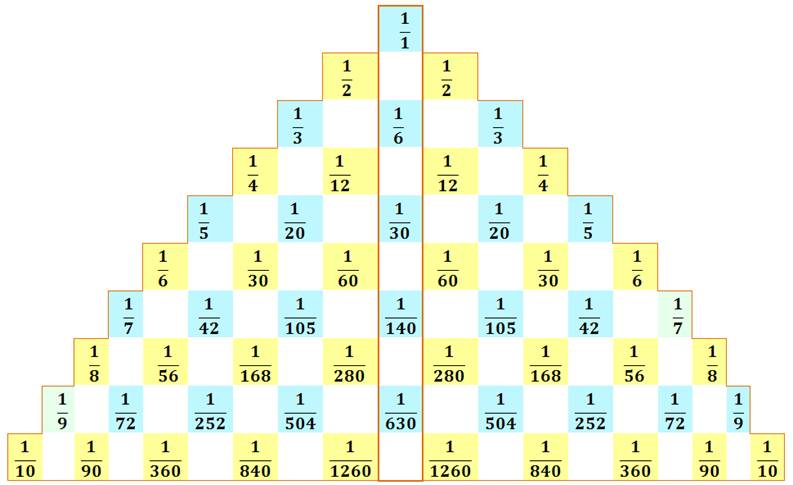
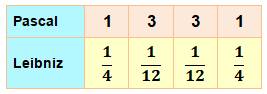
NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 18/09/2023

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths                      

            

Itérations

 

Débutants

Général

Triangles de NOMBRES

 

Glossaire

Général

 

 

INDEX

 

Triangles

 

Nombres

 

Des nombres

De Pascal

De Leibniz

 

Sommaire de cette page

>>> Série Harmonique

>>> Divergente

>>> Construction du triangle de Leibniz

>>> Propriétés

>>> Moyenne Harmonique

>>> Termes consécutifs

>>> Série sans 9

>>> Paradoxe du ver sur une bande de caoutchouc

>>> Paradoxe de l'empilement des dominos

>>> Anglais

 

 

 

 

TRIANGLE de LEIBNIZ

ou triangle harmonique

Triangle formé à partir des nombres (fractions) de la série harmonique.

Chaque ligne est constituée des inverses des termes du triangle de Pascal divisés par le numéro de la ligne (à partir de 1).

Chaque terme est la somme des deux du dessous.

 

 

 

Série Harmonique

 

*      Harmonique parce que, en musique, lorsqu'on coupe une corde en 2, on passe à l'octave au-dessus; en 3 à la quinte au-dessus; etc.

 

 

 

Cette série diverge.

Elle tend lentement vers l'infini.

 

 

Valeurs numériques

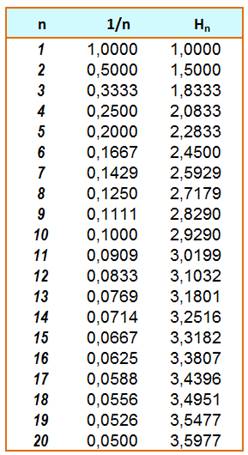
Courbe rouge: valeur des fractions successives;

En vert le cumul de la somme (Hn)

Voir Moyenne harmonique 

 

 

 

Divergente ?

 

*    Nicole Oresme (1323-1382) a eu l'idée de cette formulation dans laquelle chaque parenthèse est supérieure à 1/2.

*    Donc la suite diverge. On peut la rendre aussi grande que l'on veut en prenant le nombre de parenthèses qu'il faut. Cependant, pour ajouter 1/2 (ou à peu près), il faut doubler la quantité de nombres dans les parenthèses. Il en faut beaucoup pour croître peu.

 

*      La série diverge lentement: Pour arriver à Hn = 20, il faut:  272 400 600 termes.

 

Principe

 

Valeurs (pour information)

 

Inégalité démontrant la divergence

 

 

 

 

 CONSTRUCTION du triangle de Leibniz

 

*    La bordure gauche est construite avec les fractions successives: 1/1, 1/2, 1/3 …

*    Chaque terme interne du triangle est égal à la différence entre les deux termes à gauche. Par exemple: 1/6 = 1/2 - 1/3; 1/12 = 1/3 – 1/4; 1/1260 = 1/504 – 1/840; etc.

 

Triangle de Leibniz – Symétrique par rapport à la colonne centrale

 

 

 

Version triangle rectangle jusqu'à la vingtième ligne (partie symétrique de droite est tronquée)

En rouge la valeur ou les valeurs centrales

1

1/2

1/2

1/3

1/6

1/3

1/4

1/12

1/12

1/4

1/5

1/20

1/30

1/20

1/5

1/6

1/30

1/60

1/60

1/30

1/6

1/7

1/42

1/105

1/140

1/105

1/42

1/7

1/8

1/56

1/168

1/280

1/280

1/168

1/56

1/8

1/9

1/72

1/252

1/504

1/630

1/504

1/252

1/72

1/9

1/10

1/90

1/360

1/840

1/1260

1/1260

1/840

1/360

1/90

1/10

1/11

1/110

1/495

1/1320

1/2310

1/2772

1/2310

1/1320

1/495

1/110

1/11

1/12

1/132

1/660

1/1980

1/3960

1/5544

1/5544

1/3960

1/1980

1/660

1/132

1/13

1/156

1/858

1/2860

1/6435

1/10296

1/12012

1/10296

1/6435

1/2860

1/858

1/14

1/182

1/1092

1/4004

1/10010

1/18018

1/24024

1/24024

1/18018

1/10010

1/4004

1/15

1/210

1/1365

1/5460

1/15015

1/30030

1/45045

1/51480

1/45045

1/30030

1/15015

1/16

1/240

1/1680

1/7280

1/21840

1/48048

1/80080

1/102960

1/102960

1/80080

1/48048

1/17

1/272

1/2040

1/9520

1/30940

1/74256

1/136136

1/194480

1/218790

1/194480

1/136136

1/18

1/306

1/2448

1/12240

1/42840

1/111384

1/222768

1/350064

1/437580

1/437580

1/350064

1/19

1/342

1/2907

1/15504

1/58140

1/162792

1/352716

1/604656

1/831402

1/923780

1/831402

1/20

1/380

1/3420

1/19380

1/77520

1/232560

1/542640

1/1007760

1/1511640

1/1847560

1/1847560

 

Note sur Excel, pour obtenir les fractions indiquées, utilisez le format personnalisé que vous créer au besoin:

 

Valeurs décimales des fractions

1,0000000000

0,5000000000

0,5000000000

0,3333333333

0,1666666667

0,3333333333

0,2500000000

0,0833333333

0,0833333333

0,2500000000

0,2000000000

0,0500000000

0,0333333333

0,0500000000

0,2000000000

0,1666666667

0,0333333333

0,0166666667

0,0166666667

0,0333333333

0,1666666667

0,1428571429

0,0238095238

0,0095238095

0,0071428571

0,0095238095

0,0238095238

0,1428571429

0,1250000000

0,0178571429

0,0059523810

0,0035714286

0,0035714286

0,0059523810

0,0178571429

0,1250000000

0,1111111111

0,0138888889

0,0039682540

0,0019841270

0,0015873016

0,0019841270

0,0039682540

0,0138888889

0,1111111111

0,1000000000

0,0111111111

0,0027777778

0,0011904762

0,0007936508

0,0007936508

0,0011904762

0,0027777778

0,0111111111

0,1000000000

0,0909090909

0,0090909091

0,0020202020

0,0007575758

0,0004329004

0,0003607504

0,0004329004

0,0007575758

0,0020202020

0,0090909091

0,0909090909

0,0833333333

0,0075757576

0,0015151515

0,0005050505

0,0002525253

0,0001803752

0,0001803752

0,0002525253

0,0005050505

0,0015151515

0,0075757576

0,0769230769

0,0064102564

0,0011655012

0,0003496503

0,0001554002

0,0000971251

0,0000832501

0,0000971251

0,0001554002

0,0003496503

0,0011655012

0,0714285714

0,0054945055

0,0009157509

0,0002497502

0,0000999001

0,0000555001

0,0000416250

0,0000416250

0,0000555001

0,0000999001

0,0002497502

0,0666666667

0,0047619048

0,0007326007

0,0001831502

0,0000666001

0,0000333000

0,0000222000

0,0000194250

0,0000222000

0,0000333000

0,0000666001

0,0625000000

0,0041666667

0,0005952381

0,0001373626

0,0000457875

0,0000208125

0,0000124875

0,0000097125

0,0000097125

0,0000124875

0,0000208125

0,0588235294

0,0036764706

0,0004901961

0,0001050420

0,0000323206

0,0000134669

0,0000073456

0,0000051419

0,0000045706

0,0000051419

0,0000073456

0,0555555556

0,0032679739

0,0004084967

0,0000816993

0,0000233427

0,0000089780

0,0000044890

0,0000028566

0,0000022853

0,0000022853

0,0000028566

0,0526315789

0,0029239766

0,0003439972

0,0000644995

0,0000171999

0,0000061428

0,0000028351

0,0000016538

0,0000012028

0,0000010825

0,0000012028

0,0500000000

0,0026315789

0,0002923977

0,0000515996

0,0000128999

0,0000043000

0,0000018428

0,0000009923

0,0000006615

0,0000005413

0,0000005413

 

 

Propriétés de la Suite Harmonique

 

 

*    Alors que le triangle de Pascal a beaucoup d'applications (algèbre, dénombrement, probabilités …), celui de Leibniz en a très peu.

 

Générales

 

*    Chaque terme est aussi la somme des deux nombres du dessous:

1/12 = 1/20 + 1/30

1/20 = 1/30 + 1/60

 

*    La somme d'une diagonale infinie donne le terme initial du dessus:

1/4 = 1/5 + 1/30 + 1/105 + ...


Exemple avec onze termes

 

Relation avec le triangle de Pascal

*    Chaque terme est égal à la fraction initiale à gauche, divisé par les coefficients du triangle de Pascal.

Exemple avec 1/4

 

Propriété des colonnes

*    La somme de la première colonne est la série harmonique; elle diverge.

*    La somme de la deuxième colonne converge vers 1. Chaque terme est la moitié d'un nombre triangulaires et la somme des inverses des nombres triangulaires converge vers 2.

*    La somme de la troisième colonne converge vers 0,5. Chaque terme est le tiers d'un nombre pyramidal à base triangulaire dont la somme des inverses converge vers 3/2.

 

 Voir Triangle de Pascal

 

 

 MOYENNE Harmonique

 

Définition

 

 

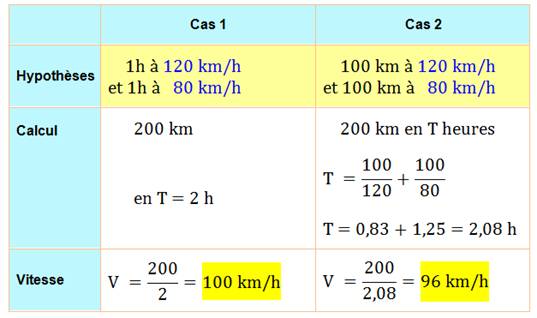
Utilisée pour les calculs avec des vitesses ou, en électricité pour les résistances.

 

Rappel

 

Longueur

= Vitesse. Temps

 

 

 

Exemples

 

 

Suite en Moyenne harmonique   /   Calculs de vitesses

 

 

 

Termes consécutifs – Produits et Sommes

Voir Nombres consécutifs

 

 

 

Série sans 9

 

*      La série harmonique privée de tous les termes comportant le chiffre 9 est convergente vers une valeur inférieure à 80.

*      Cette propriété est vraie quel que soit le chiffre ou le groupe de chiffres.
 

S = 1/1 + 1/2 + ... + 1/8 + 1/10 + ... + 1/18 + 1/20 + ... + 1/88 + 1/100 + 1/101 + …  < 80

Démonstration

 

*      Forme générique pour Sn.

 

Sn = (1/1 + ... + 1/8)
+ (1/10 + ... + 1/18 + 1/20 + ... + 1/88)
+ (1/100 + ... + 1/888) + ...
+ (1/10n−1 + ... + 1/8...8n )

 

*    Prenons cette nouvelle série dont chaque terme est plus grand que ceux de la série originelle.

 

Tn = (1/1 + ... + 1/1)
+ (1/10 + ... + 1/10)
+ (1/100 + ... + 1/100) + ...
+ (1/10n−1 + ... + 1/10n−1) > Sn

 

 

*    Quantité de nombres à k chiffres sans 9. Il y a 8 choix pour le chiffre de tête et 9 pour les k – 1 autres.

 

Q = 8 x 9k – 1

Ce qui permet de dénombrer les nombres dans chaque parenthèse.

*    Retour sur Tn

 

Tn = 8
+ 8 x 9 / 10
+ 8 x 92 / 100 + …
+ 8 x 9n – 1 / 10n – 1

 

 

*    Somme de cette série géométrique, avec 8 en facteur commun. Sa raison est 9/10 et elle a n termes.

 

 

*    Lorsque n tend vers l'infini, le terme en puissance de n (en jaune) tend vers 0.

 

 

Voir Suite des inverses des premiers

 

 

 

Paradoxe du ver sur une bande de caoutchouc

 

*    Un ver progresse sur un ruban de caoutchouc de 1 m de long.

*    vitesse du ver: 1cm / min.

*    vitesse d'étirement du ruban: 1 m / min.

*    Les vitesses sont uniformes. Est-ce que le ver atteindra le bout du ruban?

 

 

 

*    La paradoxe existe aussi en version fourmi sur une corde élastique.

 

 

La réponse est contre-intuitive, car c'est oui! Quelles que soient les vitesses, pourvu qu'elles soient constantes et, que vous ne soyez pas pressé! La durée peut dépasser l'âge de l'Univers

 

 

Le phénomène tient au fait que le ruban s'étire devant et derrière le ver, conservant la proportion de ruban déjà faite et permettant au ver de poursuivre sa progression.

La solution analytique fait intervenir la série harmonique et sa divergence (lente!).

 

Après n minutes, le rapport entre la distance parcourue par le ver et la dimension du ruban est égale à:

Lorsque ce ration atteindra la valeur 1, le ver sera au bout du ruban, alors n sera dans la zone de e100, un nombre avec quarante-trois 0.

 

Anglais: worm on a rubber band or ant on a rubber rope

Voir Paradoxes

 

 

Paradoxe de l'empilement des dominos

 

*    On connaît le jeu qui consiste à empiler des cubes pour ériger la plus haute tour.

*    Ici, le jeu va consister à les empiler pour former une tour penchée, façon pise.

*    La question est: quelle est la hauteurs maximale d'une telle tour penchée?

 

 

*    On trouve ce paradoxe de l'empilement avec des cubes, des dominos, des livres  …

Vous l'avez deviné. En adoptant en empilement harmonique, la tour peut monter à la hauteur que vous voulez sans tomber!

Mais aurez-vous assez de dominos?

 

Pour tenir l'équilibre, le centre de gravité de l'ensemble doit se projeter verticalement sur la surface du premier domino.

 

 

Anglais: Leaning tower paradox

 

 

English corner

 

The harmonic series is the inverse of the sequence of counting numbers:

1/1 + 1/2 + 1/3 + .... + 1/n....

The harmonic series grows very slowly. It diverges to infinity.

The depleted harmonic series where all of the terms in which the digit 9 appears anywhere in the denominator are removed can be shown to converge and its value is less than 80.

 

 

 

 

 

 

Suite

*         Table des nombres harmoniques

*         Triangle des nombres

*         Triangle de Pascal

*         Leibniz

*         Brève n°418

Voir

*         Boucle infernale

*         Calcul mental

*         Fractions – Index 

*         Géométrie

*         Théorie des nombres

*         Triangle – Index

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgLeibn.htm