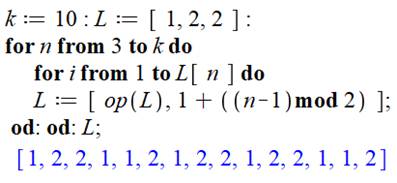|
Édition du: 27/12/2019 |
|
INDEX |
SUITES avec énumération |
|
![]()
|
SUITE DE KOLAKOSKI Suite d'Oldenbuger-Kolakoski
Suite de "1" et
de "2"
telle que chaque nombre indique la quantité de nombres à ajouter en alternant
les 1 et les 2. Connue de Rufus
Oldenburger dès 1939. William
Kolakoski (1944-1997) découvre indépendamment cette suite en 1965. |
||
|
|
Sommaire de cette page >>> Approche >>> Le démarrage >>> Propriétés >>> Programme Maple |
Débutants Glossaire |
|
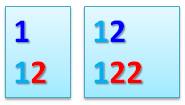
À partir de la suite déjà construite, on montre comment passer à
l'étape suivante. Les deux lignes du haut représentent:
La suite construite file plus vite que les chiffres décrivant
l'énumération.
|
Principe de la construction
En 3e ligne le 2 final indique que la quatrième ligne doit être complétée de
deux nombres. Ce seront des 2, du fait de
l'alternance 1 et 2. |
|
|
La prochaine étape consiste à prendre le 1 rose qui suit le 2 bleu de
la suite déjà construite, lequel indique qu'il faut ajouter un nombre en bout
de la suite. Ce sera un "1" du fait de l'alternance. Le suivant, après le rose, est encore un "1". Le nombre à
jouter à la fin de la suite construite est donc un seul "2". |
|
|
|
Pour bien débuter la suite, il faut
préciser la définition: Définition Les nombres de la suite indiquent la quantité de
chiffres successifs que l'on doit trouver dans la suite, généralement plus
loin dans la suite; et de plus en plus loin. Procédure
|
Première et deuxièmes étapes En haut l'état des indications déjà satisfaites. En bas, la suite construite.
Avec les indications du haut, on lit bien: il y a
un "1" et deux "2" dans la suite construite (en bas). Les trois étapes suivantes
|
|
|
La suite de Kolakoski
122112122122112112212112122112112122122112122121121122122112122122112112122
… |
||
|
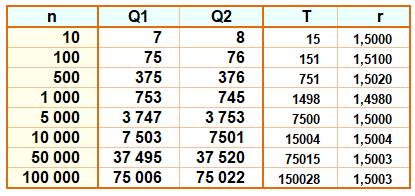
Quantité de 1 et quantité de 2
On ne sait pas prouver que la densité des "1" ou des
"2" est de 50%. |
|
||
|
Nombres formés avec la suite |
1, 12, 122, 1221, 12211,
122112, 1221121, , … 12211 est un nombre premier.
On pourrait penser que c'est le seul. Pourtant, le suivant est : 0,122112…
10283. |
||
|
Constante de Kolakoski |
Transformer les nombres de la suite en nombres
binaires en retranchant 1 à chaque chiffre et en faire un nombre à virgule: 122112122122
=> 0,11001011011 … Ce nombre
binaire converti en décimal devient une constante: 0,79450719268061220646 …
Voir Conversion Maple |
||
|
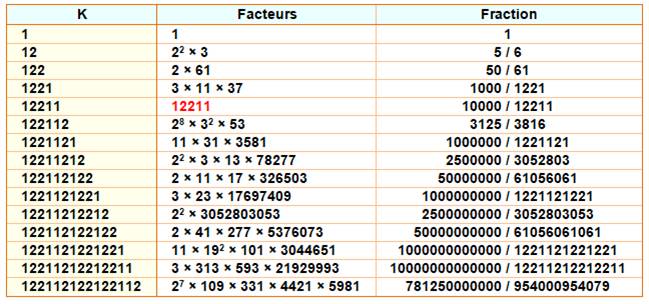
Table des premiers nombres formés
par la suite de Kolakoski et leurs facteurs
Cette suite ne possède pas de motifs répétitifs, tout
comme les nombres irrationnels. |
|||
|
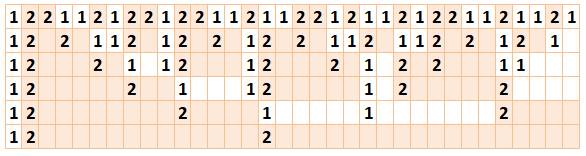
La suite est fractale |
Elle se décrit elle-même,
y compris à différente échelles. |
||
|
|
|||
|
La suite est généralisable |
La suite
présentée est construite avec l'alphabet 1, 2. La suite avec
l'alphabet 1, 3 serait: 1, 3, 3, 3, 1, 1, 1, 3, 3, 3, 1, 3, 1, 3, 3, 3,
1, 1, 1, 3, 3, 3, 1, 3, 3, 3, 1, 3, 3, 3, 1, 1, 1, 3, 3, 3, … (Michel Dekking – 2018) 13, 1331,
13331113331 sont des nombres premiers |
||
|
Programme
Première étape du traitement n = 3 => 1 + (3 – 1) mod 2 = 1 + 0 = 1 L[3 ] = 2 => ce nombre est à ajouter deux
fois. Deuxième étape du traitement n = 4 => 1 + (4 – 1) mod 2 = 1 + 1 = 2 L[4 ] = 1 => ce nombre est à ajouter une fois. |
Commentaires Recherche des 10 premiers nombres de la suite (k
= 10). Liste initiale 1, 2, 2 en L. Boucle d'exploration des nombres de 3 à k = 10. Boucle qui introduit un ou deux chiffres selon la
valeur de l'indicateur en L(n). Le chiffre introduit à l'aide d'u calcul
d'alternance égal à 1 plus une valeur
complémentaire qui vaut 0 ou 1 selon la valeur de n. Le principe est que le nombre alterne chaque fois
que l'on passe à l'étape suivante, au n suivant. |
|
|
1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1,
2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1,
2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2,
1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1,
2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1,
1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2,
1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1,
2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1,
2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2,
1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1,
2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1,
2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1,
1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1,
2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1,
1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1,
1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2,
1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1,
2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 2,
1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2,
2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1,
1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2,
1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1,
1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2,
1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2,
2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1,
2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2,
1, 2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1,
2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 2,
1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2,
1, 1, 2, 2, 1, 2, … |
|
Cumul de la somme des nombres de la
suite 1, 3, 5, 6, 7, 9, 10, 12, 14, 15, 17, 19, 20, 21,
23, 24, 25, 27, 29, 30, 32,
33, 34, 36, 37, 39, 41, 42, 43, 45, 46, 47, 49, 50, 52, 54, 55, 57, 59, 60,
61, 63, 64, 66, 68, 69, 71, 72, 73, 75, 76, 77, 79, 81, 82, 84, 86, 87, 88,
90, 91, 93, 95, 96, 98, 100, 101, … |
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Suite/aSuite/Kolakosk.htm
|