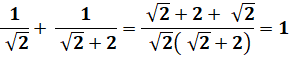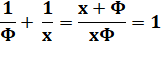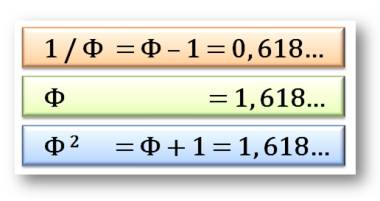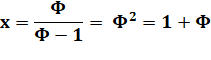|
|||||||||||||||||||||||||||||
![]()
|
Spectre
numérique d'un
nombre réel Suite de nombres caractérisant un nombre rationnel. Objet de curiosités avec sa suite
complémentaire. |
|
|
|
|
Théorème Si deux nombres sont complémentaires harmoniques (la somme de
leur inverse est égal à un) alors leur spectre forment la suite exacte des nombres
entiers. |
|
|
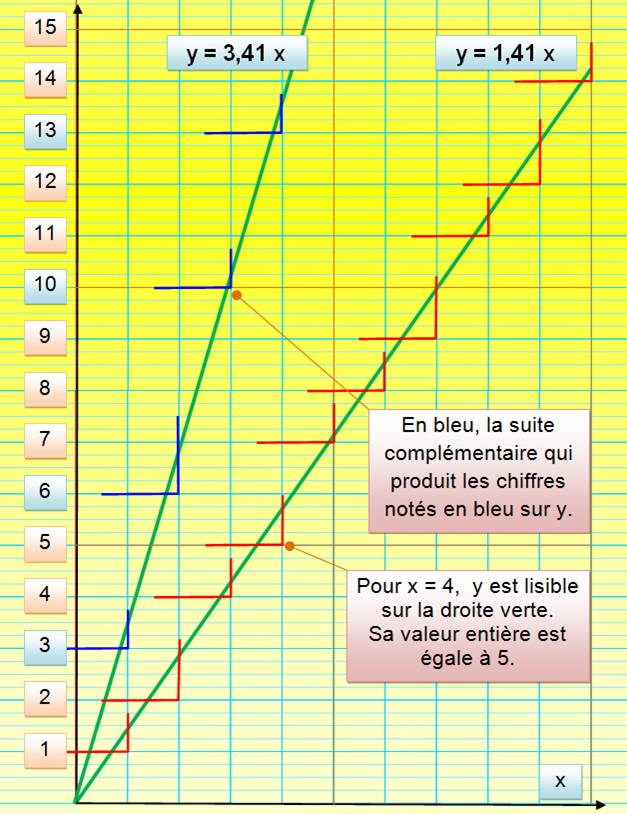
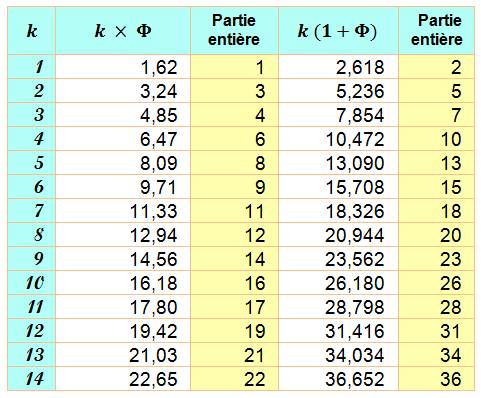
Illustration graphique
|
|
|
|
|
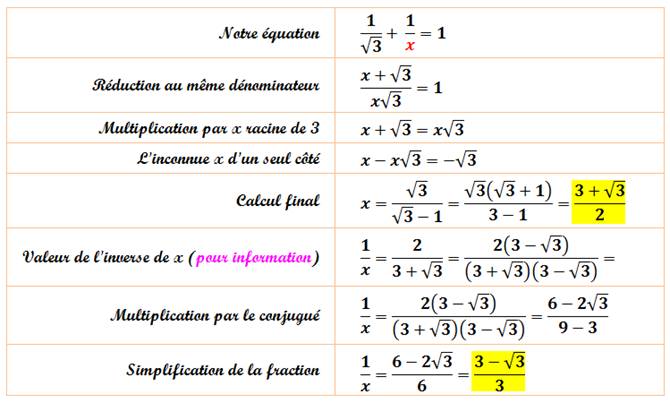
Voir Calcul
algébrique
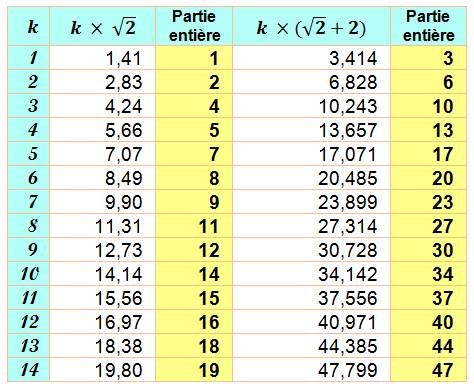
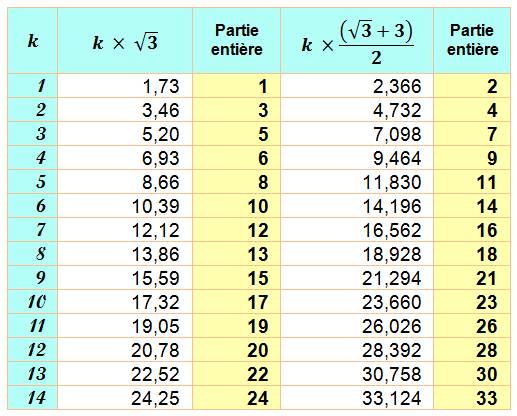
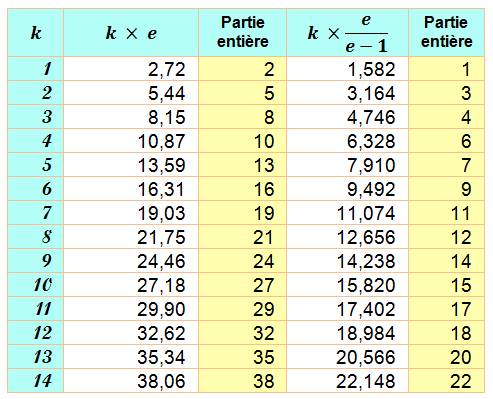
Notre règle du spectre
complémentaire fonctionne bien. Nous retrouvons la suite des nombres entiers
en utilisant les deux colonnes en jaune. |
|
|
|
|
|
|
|
Voir
Suite binaire dorée et Fibonacci
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Suite/aSuite/SpectNum.htm |
![]()