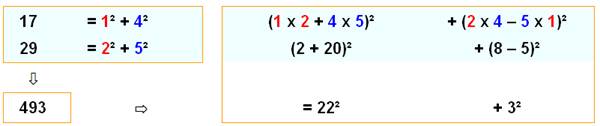|
||||||||||||||||||||||||||
![]()
|
NOMBRES COMPLEXES Somme de carrés Amusement avec les nombres imaginaires pour former des
sommes de deux carrés. Où un passage par
les complexes donne un résultat réel. |
Voir page semblable: Identité de Brahmagupta –
Fibonacci
|
|
|
|
Voyez
ce tableau:
200 = 14² + 2² = 10 x 20 = (1² + 3²) (2² + 4²) En
appliquant la recette indiquée, cela marche à tout coup!
493 = 22² + 3² = 17 x 29 = (1² + 4²) (2² + 45²) |
|
|
|
||
|
La
somme des carrés de deux nombres réels est égale au produit de deux nombres
complexes conjugués. La
magie de la recette donnée ci-dessus
tient à cette identité! |
En effet (a + ib)
(a – ib) = a² + i ab – i
ab – i² b² = a² + b² |
|
Voir Identités
complexes / Identités remarquables
|
|
|
|
Utilisons
l'identité pour les deux petites sommes de carrés.
Puis
multiplions les résultats en groupant de la façon indiquée. On
effectue le calcul des produits à droite et à gauche. On
se souvient que i² = – 1. Et
pour finir, on réutilise notre identité pour transformer le produit des
conjuguées en une somme de deux carrés. |
|
|
|
||
|
(a² + b²) (c² + d²) = N
= E² +
F²
En italique, cas où E ou F = 0
(possible si N est un carré) En rouge, première présent |
||
Voir Suite de la table jusqu'à 500
/ Table complète
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()