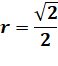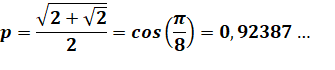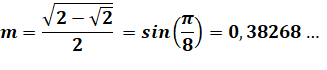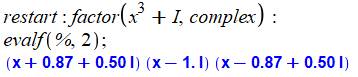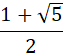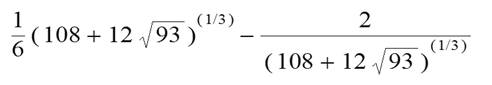|
||||||||||||||||||||||||||
![]()
|
|
|||
|
x² + 1 x3 + x² + x +
1 x3 – x² + x – 1 x4 + 1 x6 + 1 |
= = = = = |
(x – i) (x + i) (x + 1) (x + i)
(x – i) (x – 1) (x + i)
(x – i) (x² + i) (x² – i) (x3 + i) (x3
– i) |
|
|
x² + 1 x² – 1 |
= = |
(x – i) (x + i) (x – 1) (x + 1) |
|
|
x² + i x² – i |
= = |
(x – r.i + r) ( x + r.i – 1) (x – r.i – r) ( x + r.i + 1) |
|
|
x² + 4 4x² + 1 |
= = |
(x – 2i) (x + 2i) (2x – i) (2x + i) |
|
|
x3 + 1 x3 – 1 |
= = |
(x + 1) (x² – x + 1) (x – 1) (x² + x + 1) |
|
x3 + i x3 – i |
= = |
(x – i) (x² + ix – 1) (x + i) (x² – ix – 1) |
|
x3 + x |
= = |
x
(x – i) (x + i) x (x – 1) (x + 1) |
|
x3 + 2x² + x + 1 x3 + 2x² + x + 2 x3 + 3x² + x + 3 |
= = = |
(x + 1) (x + i)
(x – i) (x + 2) (x + i)
(x – i) (x + 3) (x + i)
(x – i) |
|
x4 + 1 x4 – 1 |
= = = |
(x² + i) (x² – i) (x² + 1) (x² – 1) (x – i) (x + i) (x – 1) (x + 1) |
|
x4 + i x4 – i |
= = |
(x+p-i.m) (x+m+r.p) (x-m+p.i)
(x-p+m.i) (x+p+i.m) (x+m-r.p) (x-m+p.i)
(x-p-m.i) |
|
|
|
x5 + 1 x5 – 1 |
= = |
(x + 1) (x4 – x3
+ x2 – x + 1) (x – 1) (x4 + x3
+ x2 + x + 1) |
|
x5 + i x5 – i |
= = |
(x + I) (x4 – i.x3
– x2 + i.x + 1) (x – I) (x4 + i.x3
– x2 – i.x + 1) |
|
x5 + x4 + x
+ 1 x5 – x4 + x
– 1 |
= = |
(x + 1) (x² + i) (x² – i) (x – 1) (x² + i) (x² – i) |
|
x6 + 1 x6 – 1 |
= = |
(x² – ix – 1) (x² + ix – 1) (x –
i) (x + i) (x² – x + 1) (x² + x + 1) (x – i)
(x + i) |
|
x6 + i x6 – i |
= = |
(x2 – i) (x4
+ i.x2 – 1) (x2 + i) (x4
– i.x2 – 1) |
|
x6 + x4 + x²
+ 1 |
= = |
(x² + 1) (x² + i) (x² – i) (x² + 1) (x² + i) (x – i) (x + i) |
Logiciels
|
La factorisation complexe s'obtient avec:
|
|
Avec Maple, on peut aussi obtenir une factorisation plus poussée
(mettre complex au lieu de I):
|
Voir Calculs
autour de i
|
|
||||
|
Polynôme & sa factorisation |
=> |
Réelle |
Complexe |
|
|
x² + 1 |
= |
|
(x + i) (x –
i) |
|
|
x² – 1 |
= |
(x + 1) (x –
1) |
|
|
|
x² + x + 1 |
= |
|
(x + 0,5 + 0,866i*I) (x + 0,5 – 0,866*I) |
|
|
x² + x – 1 |
= |
(x + 1,618)
(x – 0,6180) |
|
|
|
x² – x – 1 |
= |
(x – 1,618) (x + 0,6180) |
|
|
|
x3 + 1 |
= |
|
(x + 1) (x – 0,5 + 0,866*I) (x – 0,5 – 0,866*I) |
|
|
x3 – 1 |
= |
|
(x – 1) (x + 0,5 + 0,866*I) (x + 0,5 – 0,866*I) |
|
|
x3 + x |
= |
|
(x + 0) (x +
i) (x – i) |
|
|
x3 – x |
= |
(x –1) x (x + 1) |
|
|
|
x3 + x + 1 |
= |
|
(x + 0,682) (x – 0,341 + 1,162*I) (x – 0,341 – 1,162*I) |
|
|
x3 + x – 1 |
= |
|
(x – 0,682) (x + 0,341 + 1,162*I) (x + 0,341 – 1,162*I) |
|
|
x3 + x² + x + 1 |
= |
|
(x + 1) (x +
i) (x – i) |
|
|
x3 + x² + x – 1 |
= |
|
(x – 0,543) (x + 0,771 + 1,11*I) (x + 0,771 – 1,11*I) |
|
|
x3 + x² – x – 1 |
= |
(x + 1)² (x – 1) |
|
|
|
x3 –
x² + x – 1 |
= |
|
(x – 1) (x + i) (x – i) |
|
|
x4 + 1 |
= |
|
(x² + i) (x² – i) |
|
|
x4 + x + 1 |
= |
|
(x + 0,727 + 0,43*I) (x + 0,727 – 0,43*I) (x – 0,727 + 0,934*I) (x – 0,727 – 0,934*I) |
|
|
x4 + x² + x + 1 |
= |
|
(x + 0,547 + 0,585*I) (x + 0,547 – 0,585*I) (x – 0,547 + 1,121*I) (x – 0,547 – 1,121*I) |
|
|
x4 + x3 + x² + x + 1 |
= |
|
(x + 0,809 + 0,587*I) (x + 0,809 – 0,587*I) (x – 0,309 + 0,951*I) (x – 0,309 – 0,951*I) |
|
|
x5 + 1 |
= |
|
(x + 1) (x + 0,309 + 0,951*I) (x + 0,309 – 0,951*I) (x – 0,809 + 0,587*I) (x – 0,809 – 0,587*I) |
|
|
x5 + x4 + x + 1 |
= |
|
(x + 1) (x² + i) (x² – i) |
|
|
x5 + x4 + x3 + x² x + 1 |
= |
|
(x + 1,25) (x + 0,315 + 1,051*I) (x + 0,315 – 1,051*I) (x – 0,440 + 0,6863*I) (x – 0,440 – 0,6863*I) |
|
|
x6 + 1 |
= |
|
(x3 + i) (x3 – I) |
|
|
x6 + x4 + x² + 1 |
= |
|
(x² + 1) (x² + i) (x² – i) |
|
|
Explicitation des nombres
ci-dessus |
|
||
|
0,8660254040… |
= |
|
|
|
1,618033989… |
= |
|
|
|
0,6823278040… =
|
|||
|
0,6823278040… |
= |
A/6 - 2 /A |
|
|
0,3411639019… |
= |
A/3 - 1/A |
|
|
1,161541400 … |
= |
A/3 + 1/A |
|
|
0,5436890125… |
= |
A/3 - 2/3A - 1/3 |
|
|
-0,7718445065… |
= |
-A/6 + 1/3A - 1/3 |
|
|
-1,115142508… |
= |
- (A/3 + 2/3A ) Ö3/2 |
|
Nous avons atteint la puissance 3
Avec les puissances supérieures les
expressions sont plus compliquées!
Ce qui montre que les factorisations
données ci-dessus ne sont pas très faciles à calculer
|
|
|
|
x² + 1 = (x + 1,000000000*I) (x
- 1,000000000*I) x² + 2 = (x + 1,414213562*I) (x
- 1,414213562*I) x² + 3 = (x + 1,732050808*I) (x
- 1,732050808*I) x² + 4 = (x + 2,000000000*I) (x
- 2,000000000*I) x² + 5 = (x + 2,236067977*I) (x
- 2,236067977*I) x² + 6 = (x + 2,449489743*I) (x
- 2,449489743*I) x² + 7 = (x + 2,645751311*I) (x
- 2,645751311*I) x² + 8 = (x + 2,828427125*I) (x
- 2,828427125*I) x² + 9 = (x + 3,000000000*I) (x
- 3,000000000*I) x² + 10 = (x + 3,162277660*I) (x
- 3,162277660*I) |
|
|
|
|
|
x3 + 1 = (x +
1) (x - 0,5 + 0,866*I) (x - 0,5 - 0,866*I) x3 + 2 = (x +
1,260) (x - 0,6300 + 1,091*I) (x - 0,6300 - 1,091*I) x3 + 3 = (x +
1,442) (x - 0,7211 + 1,249*I) (x - 0,7211 - 1,249*I) x3 + 4 = (x +
1,587) (x - 0,7937 + 1,375*I) (x - 0,7937 - 1,375*I) x3 + 5 = (x +
1,710) (x - 0,8550 + 1,481*I) (x - 0,8550 - 1,481*I) x3 + x2 + 4 = (x+2)
(x - 0,5 + 1,323*I) (x - 0,5 - 1,323*I) |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()