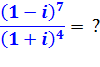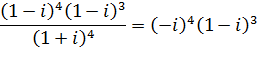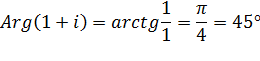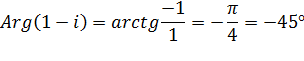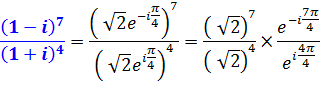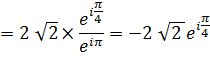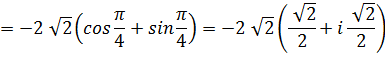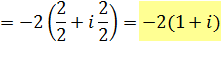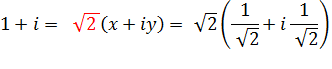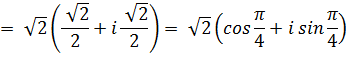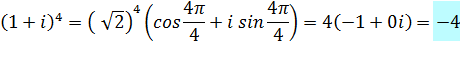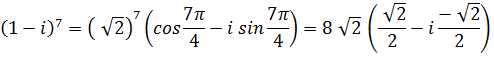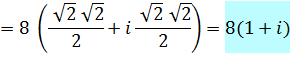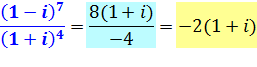NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 18/01/2016

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

Nombres complexes

 

Débutants

Complexes

PUISSANCE

 

Glossaire

Complexe

 

 

INDEX

 

Complexes

Réelle (principes)

Réelle (calculs)

Imaginaire

Réelle entière

Réelle (gd nombre)

Complexe

 

Sommaire de cette page

>>> Résolution avec identités remarquables

>>> Résolution selon plusieurs méthodes

 

 

 

PUISSANCE réelle

d'un nombre complexe

Exemples de CALCULS

 

 

 

Identités remarquables

(2 + 3i)2

= 22 + 2 x 2 x 3i + (3i)2

= 4 + 12i – 9

= – 5 + 12i

(2 – 3i)2

= 4 – 2 x 2 x 3i + 3i x 3i

= 4 – 12i – 9

= – 5 – 12i

(2 + 3i) (2 – 3 i)

= 22 – (3i)2

= 4 – ( 9i2)

= 4 + 9 = 13

(2 + 3i)3

= 23 + (3 x 22 x 3i) + (3 x 2 x (3i)2) + (3i)3

= 8 + 36i + (6 x 9 x i2) + (27 x i2 x i)

= 8 + 36i – 54 – 27i

= – 46 + 9i

(2 + 3i)3

= 23 + (3 x 22 x 3i) + (3 x 2 x (3i)2) + (3i)3

= 8 + 123i + (6 x 3 x i2) + (33 x i2 x i)

= 8 + 123i – 18 – 33i

= – 10 + 93i

(2 + 3i)3

= (2)3 + (3 x (2)2 x 3i) + (3 x 2 x (3i)2) + (3i)3

= 22 + 63i + (32 x 3 x i2) + (33 x i2 x i)

= 22 + 63i – 92 – 33i

= – 72 + 33i

(1 + 3i)3

= 13 + (3 x 12 x 3i) + (3 x 1 x (3i)2) + (3i)3

= 1 + 33i + (3 x 3 x i2) + (33 x i2 x i)

= 1 + 33i – 9 – 33i

= – 8

Voir Identités remarquables

 

 

 

Résolution selon trois méthodes

 

Calculez

 

 

Forme cartésienne

 

 

Passage à la forme exponentielle

Plus fastidieuse mais universelle.

 

Calculs des modules et arguments

 

 

 

 

 

Calcul de la division

 

 

 

 

Forme trigonométrique
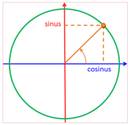
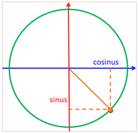
pour revenir à la forme cartésienne

 

 

Passage à la forme trigonométrique directement

Pour retrouver les valeurs des sinus et cosinus, imaginez la position du point sur le cercle.

 

 

Calcul de la puissance

Rappel: Angle , son cosinus est -1 et son sinus est 0.

 

Calcul de l'autre puissance

Rappel: Angle , son cosinus est  et son sinus est .

 

Division demandée

Voir Formes des nombres complexes

 

 

 

 

Suite

*         Puissances imaginaires

*         Complexe – Index

Voir

*         Constantes

*         Construction de l'heptagone

*         Inventaire des types de nombres

*         Nombre de Gauss

*         Nombres – Glossaire et index

*         Nombres d'Eisenstein

*         Nombres périodiques

*         Nombres réels

*         Puissances et racines – Index

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/PuisReCa.htm