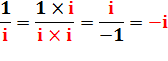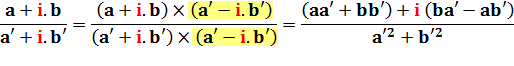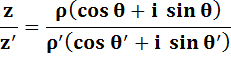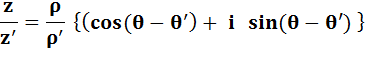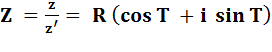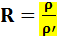|
|||||||||||||||||||||||||||
![]()
|
Nombres complexes DIVISIONS |
|
|
||
|
Approche |
La multiplication multiplie les modules et ajoutent les
arguments. Sans surprise, la division divise les modules et
soustrait les arguments. Le calcul d'une division de nombres complexes fait
appel au conjugué
du numérateur. |
|
|
Le plus simple! |
|
|
|
Cartésien |
Exemple: z = 1,4 + 0.4
i; z' = 0,8 + 0,8 i
= 1,4 x 0,8 + 0,4 x 0,8 + i (0,4 x 0,8 –
1,4 x 0,8) = 1,44
– 0 ,8 i D = 0,8² + 0,8² =
1,28 Z = 1,44 / 1,28 –
0,8 / 1,28 = 1,125 – 0,625 i |
|
|
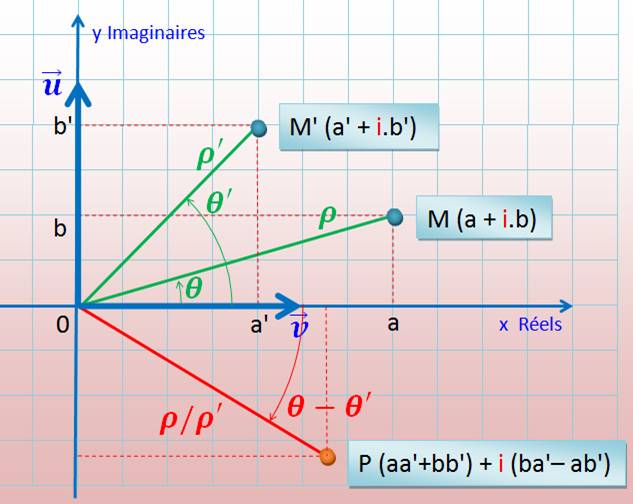
Illustration |
u et v
sont les vecteurs unitaires portés par les deux axes |
|
Polaire |
Diviser deux nombres complexes, c'est diviser leur
modules (longueurs) et soustraire les arguments (angles).
avec Exemple
– Calcul du module
R
= 1,4560 / 1,1313 = 1,2870… R²
= 1,125² + 0,625² = 1,265 + 0,3906 = 1,6562 => R = 1,2870… Exemple
– Calcul de l'argument
R = arctg (-0,625 / 1,125) = 1,0637 => -29,054° |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Division.htm |
![]()