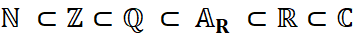|
|||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|||
|
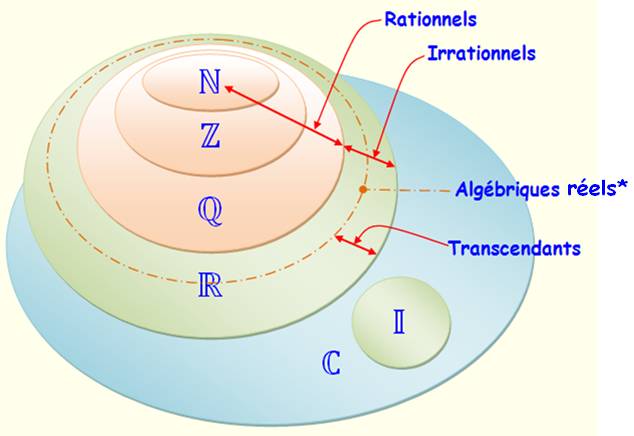
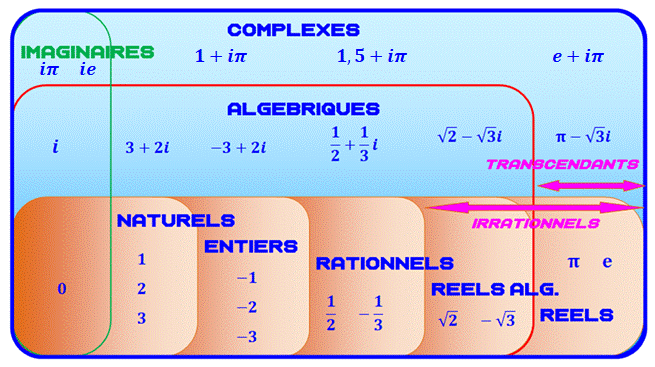
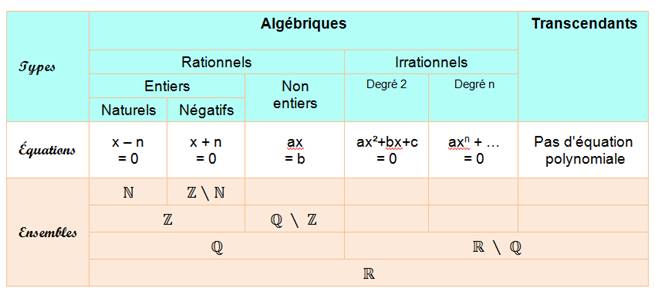
*Note: il existe aussi des nombres algébriques complexes. Voir Diagramme ci-dessous. Autre
présentation (diagramme d'Euler)
Relations
Graphe avec exemples de nombres
Voir Définition de chacun / Nombres
décimaux / Développement décimal |
|||
Notez bien que "i" est situé dans
l'ensemble des nombres complexes; il n'est pas
irrationnel
Précisions sur le bas de ce tableau
|
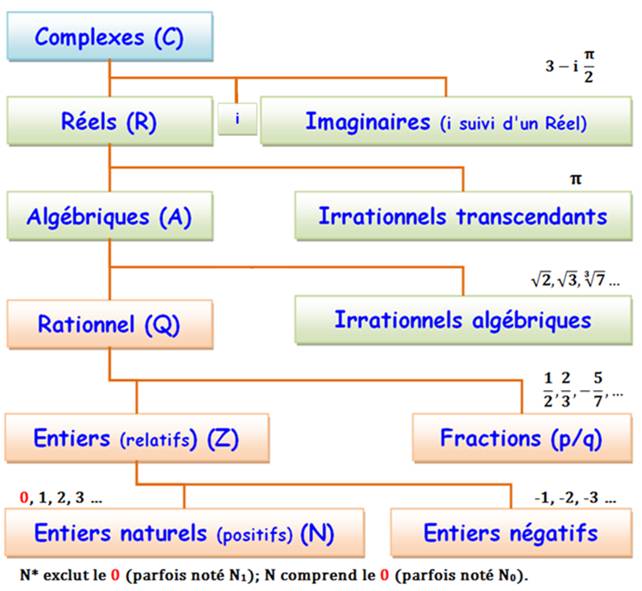
1)
Rationnel est un autre mot pour dire fractions.
Toutes sortes de fractions:
2)
Justement, parmi les rationnels, les
fractions au sens large, on peut distinguer:
3) Finalement, les entiers relatifs, les nombres peuvent être
|
Merci à José Luis I.
D'après une présentation de Norbert Verdier
Un autre ensemble particulier de nombres
|
C'est le groupe des
unités de |
![]()
|
Retour |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()