NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/10/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres complexes
Débutants Complexes	Opérations			Glossaire Complexe
INDEX Complexes	Opérations	Addition	Multiplication
		Soustraction	Division
		Sommaire de cette page >>> Multiplication >>> Exemple >>> Interprétation géométrique >>> Carré de 1 + i >>> Anglais

Nombres complexes MULTIPLICATIONS

MULTIPLICATION
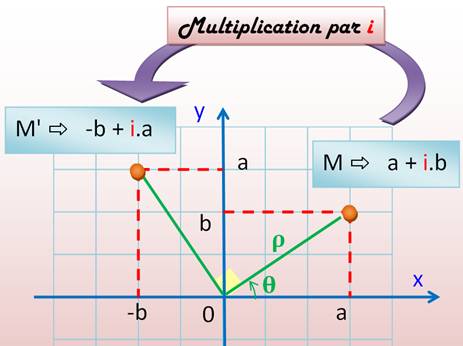
Par i	La multiplication par i correspond à une rotation antihoraire de 90°.
Formule	(a + i.b) . i	= i . a + i² . b = – b + i . a
Illustration
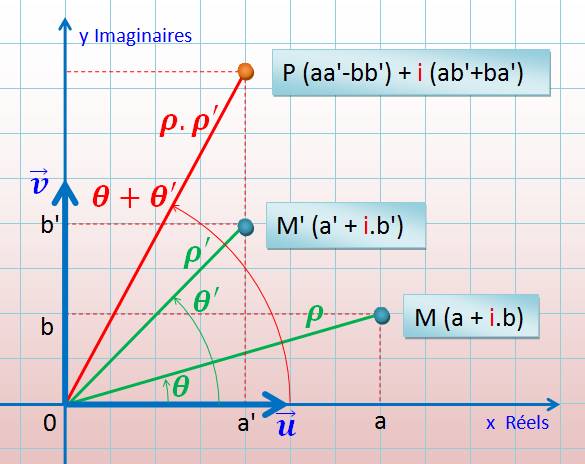
Générale	(a + i.b) x (a' + i.b')		= (aa' – bb') + i (ab' + ba')
Cas particulier	(a + i.b) x (a – i.b)		= a² + b²
Propriété	La multiplication dans le monde des complexes conserve la multiplication classique des modules (de la longueur des segments représentants les nombres complexes).
Calcul économe	Calcul du produit de deux nombres complexes avec seulement trois multiplications, au lieu de quatre: Partie réelle: Re = aa' – bb' Partie imaginaire: Im = (a + b)(a' + b') – aa' – bb'

Voir Table de multiplication de 1, i et -1

Exemples
(4 + 2i) (4 – 2i) (4 + 2i)^2 (4 – 2i)^2 (1 + i) (2 + i) (3 + i) (1 – i) (2 – i) (3 – i) (1 + i) (2 + i) (3 + i) (4 + i) (1 – i) (2 – i) (3 – i) (4 – i)	= 4² + 2² = 20 = 4^2 + 2 x 4 x 2 i + 2^2 i^2 = 16 + 16i – 4 = 12 + 16i = 4^2 – 2 x 4 x 2 i + 2^2 i^2 = 16 – 16i – 4 = 12 – 16i = (1+ i) (6 + 2i + 3i + i^2) = (1+ i) (5 + 5i ) = 5 + 5i + 5i + 5i^2 = 10i = – 10i = – 10 + 40i = – 10 – 40i
Pour s'entraîner

Interprétation géométrique
Cartésien	Exemple: z = 1,4 + 0.4 i; z' = 0,8 + 0,8 i z.z' = a.a' – b.b' + i (a.b' + b.a') = 1,4 x 0,8 – 0,4 x 0,8 + i (1,4 x 0,8 + 0,4 x 0,8) = 0,8 + 1,44 i
Illustration	u et v sont les vecteurs unitaires portés par les deux axes
Polaire	Voir Identités trigonométriques Multiplier deux nombres complexes, c'est multiplier leur modules (longueurs) et ajouter les arguments (angles). avec Exemple – Calcul du module = 1,4² + 0,4² = 1,96 + 0,16 = 2,12 => = 1,4560… = 0,8² + 0,8² = 0,64 + 0,64 = 1,2 => = 1,1313… R = 1,4560 x 1,1313 = 1,6473… Vérification avec les coordonnées cartésiennes: R² = 0,8² + 1,44² = 0,64 + 2,07 = 2,71 => R = 1,6473… Exemple – Calcul de l'argument = arctg (0,4 / 1,4) = 0,278 => 15,94° = arctg (0,8 / 0,8) = 0,785 => 45° R = arctg (0,8 / 1,44) = 1,0637 => 60,94°

Cas du complexe 1 + i ou 1 - i
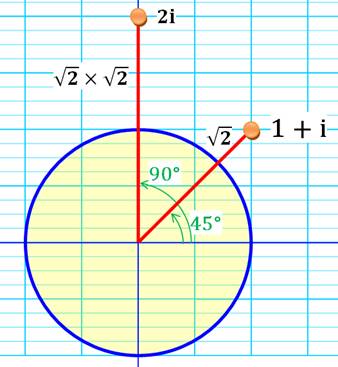
Le carré de ces deux nombres complexes est typiquement imaginaire. (1 + i)² = 1² + 2i + i² = 1 + 2i – 1 = 2i (1 – i)² = 1² – 2i + i² = 1 – 2i – 1 = –2i Graphiquement: le point est en 1 + i et le module vaut : et l'argument vaut 45°. Le carré est donc le point ayant pour module et l'argument vaut 45 + 45 = 90°. Soit la formule:

Voir Calculs avec 1 + i

English Corner
The modulus of the product of two complex numbers is product of their moduli, and the argument of the product of any two complex numbers is the sum of their arguments

Suite	Division complexe Multiplication ordinaire Nombres complexes – Index
Voir	Inventaire des types de nombres Nombres – Glossaire et index Nombres réels Opérations – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Multipli.htm