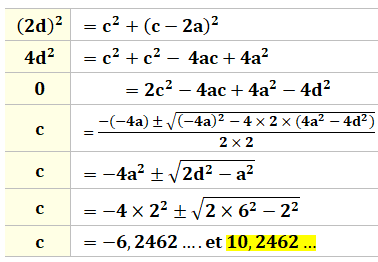Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 18/08/2023 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Nappe sur table	Deux demi-cercles
	Coin du carré replié	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Trois triangles réunis
	Carré coupé en quatre	Cercle et demi-cercle	Défis divers

Carré coupé en quatre par deux sécantes Deux sécantes symétriques dans un carré. Calculer l'aire.
	Sommaire de cette page >>> Le carré coupé en quatre	Débutants Géométrie Glossaire Géométrie

Le carré coupé en quatre		haut
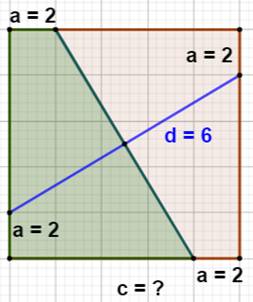
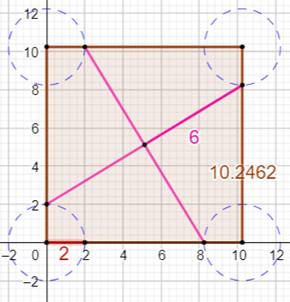
Construction Un carré. Un point sur chaque côté à a = 2 du sommet en tournant dans le sens des aiguilles d'un montre. Une des sécantes est distante de d = 6 du point de concours et du côté. Quelle est l'aire du trapèze rectangle vert ? Principe de la solution géométrique Les deux sécantes sont symétriques; elles se coupent el leur milieu. Elles mesurent donc 2 × 6 = 12. Prenons la sécante bleue, elle est inscrite dans un rectangle de longueur c et de largeur c – 2a et dont la diagonale vaut 12. Un coup de Pythagore et le tour est joué ! Calculs

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CarrCoup.htm