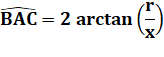Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/02/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Cercle et trg rectangle	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Trois triangles réunis
	Cercle dans le secteur	Cercle et demi-cercle	Défis divers

Cercle dans le secteur Problème de géométrie très simple. La subtilité réside dans l'obtention de la présentation du résultat.
	Sommaire de cette page >>> Cercle dans le secteur >>> Deux cercles dans le secteur	Débutants Géométrie Glossaire Géométrie

Cercle dans le secteur		haut
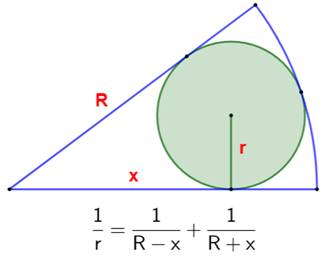
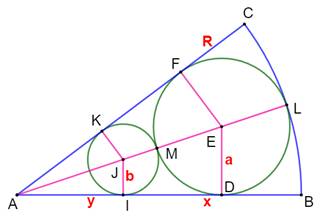
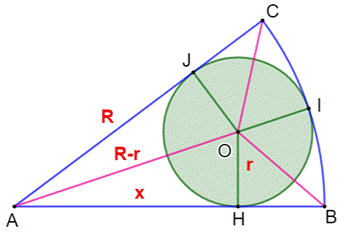
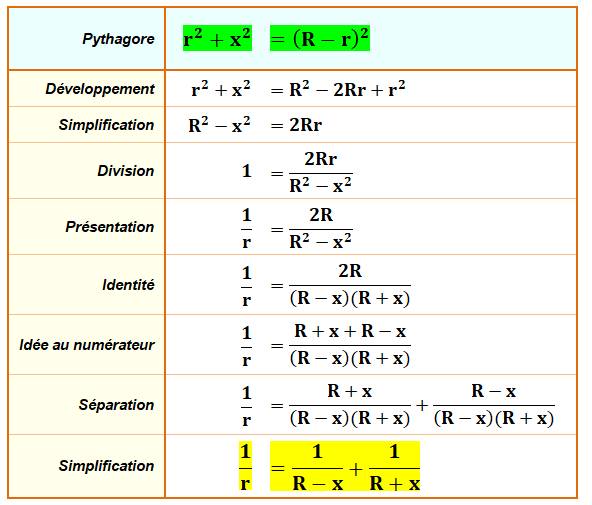
Construction Un secteur de rayon R et d'angle quelconque. Le cercle inscrit dans ce secteur; son rayon est r. La distance du sommet du secteur au point de tangence est noté x. Démontrer la relation indiquée entre R, r et x. Piste Une relation évidente est établie dans le triangle rectangle AHO avec le théorème de Pythagore. La suite est simplement une question d'arrangement calculatoire de la relation. Angle du secteur (BAC) – Pour info	Figure initiale Figure avec notations
Calculs

Voir Brève 61-1203

Deux cercles dans le secteur		haut
Relations pour résoudre les deux cercles	Figure avec notations
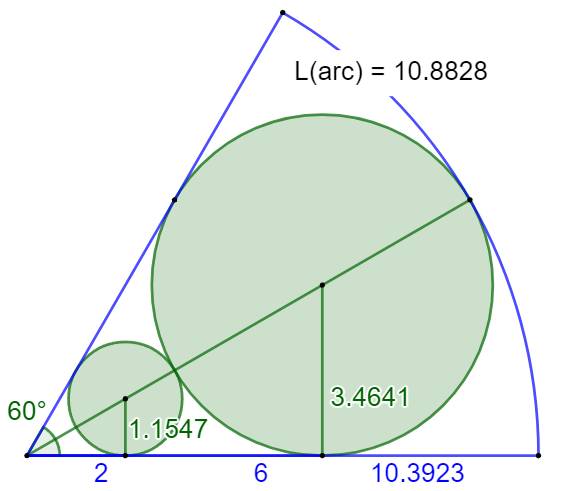
Exemple de résolution

Haut de page

Retour	Autres défis Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CerSect.htm