Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 26/01/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Trois triangles réunis
	Fourmi sur un pavé	Cercle et demi-cercle	Défis divers
	Cercle sur équerre	Quarts de cercle

Quarts de cercles
	Sommaire de cette page >>> Demi-cercle dans le quart de cercle >>> Demi-cercle dans le quart de cercle >>> Cercle inclus dans une figure avec quart de cercle	Débutants Géométrie Glossaire Géométrie

Demi-cercle dans le quart de cercle		haut
Problème qui se résout en dessinant une sorte de quadrillage révélateur. Les milieux jouent un rôle primordial.
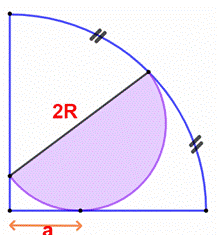
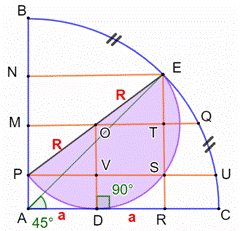
Construction Un quart de cercle dans lequel est inscrit un demi-cercle. Les deux arcs de cercle sont de même longueur. Calculer la relation entre le rayon R et la longueur a. Piste Le point O est le milieu du diamètre PE, alors le point D est le milieu de AR et AD = DR = a. Le point E est le milieu de l’arc BC ; La droite AE est la bissectrice de l’angle droit CAB ; L’angle CAE vaut 45° ; par conséquent RA = RE = 2a et ET = 2a – R. Notez le quadrillage orange Triangle OTE Dans le triangle rectangle OTE, avec Pythagore : OE² = OT² + TE² R² = a² + (2a – R)² R² = a² + 4a² – 4aR + R² 5a² = 4aR R = 5a / 4	Figure initiale Figure avec notations

Demi-cercle dans le quart de cercle		haut
La piste à suivre pour résoudre ce cas est finalement simple mais ne saute pas forcément aux yeux.
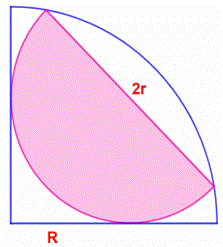
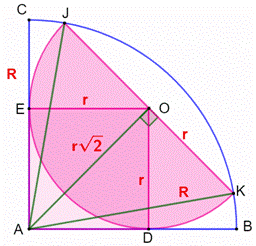
Construction Un demi-cercle de rayon r, inscrit dans un quart de cercle de rayon R. Les points de tangence sont situés sur les côtés du quart de disque. Quelle est la relation entre R et r ? Piste Le centre O du demi-cercle est à égale distance des côtés de tangence sur AB et sur AC. Alors, OD = OE = r Le quadrilatère ADOE est un carré. Sa diagonale mesure : r √2 Triangle KAJ Le triangle KAJ est isocèle car AK = AJ = r Le point O est le centre du demi-cercle et OJ = OK. Le segment AO est la médiane issue du sommet du triangle isocèle KAJ. Il est aussi hauteur et médiatrice. L’angle AOK est droit. Notez que nous venons de démontrer que la figure est symétrique par rapport à la droite AO. Calcul du rayon R Dans le triangle rectangle AOK, avec le théorème de Pythagore : AO² = AK² – OK² 2r² = R² – r² R² = 3r² R = √3 r	Figure initiale Figure avec notations

Cercle inclus dans une figure avec quart de cercle		haut
Problème qui comporte de nombreux calculs. Un passage pas l’évaluation des angles (tangente) et un peu de trigonométrie est nécessaire. Pas très évident de trouver le bon angle d’attaque !
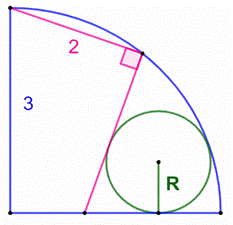
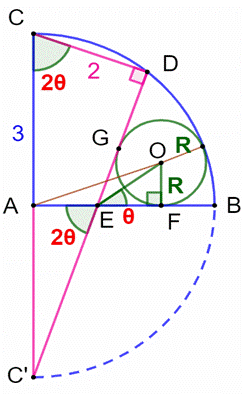
Construction Un quart de cercle de rayon 3 cm. Un quadrilatère avec deux angles droits opposés dont un des côté mesure 2cm. Un cercle est logé dans l’espace libre, tangent en trois points. Quel est le rayon de ce cercle? Piste Tout d’abord, il vient naturellement à l’esprit de prolonger le quart de cercle et de former le triangle CDC’, inscrit dans un demi-cercle, donc rectangle. Le point O, centre du petit cercle est situé sur la bissectrice de l’angle BED (cf. tangence en F et G). On a : ^OEF = ^OEG = θ L’idée consiste à calculer R à partir de cet angle : R = EF· tanθ	Figure initiale
Calcul de l’angle thêta Pour évaluer l’angle thêta, on va remarquer que son double se trouve dans le triangle CDC’ en CDC’ comme en AEC’. Or ce triangle est connu. (On utilisera l'identité des angles doubles)	Figure avec notations

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	A Very Nice Math Olympiad Geometry Problem | Given a circle inside a quarter circle – Math Booster
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/QuartCer.htm