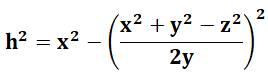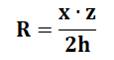|
Édition du: 26/01/2025 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
Calculer le rayon Calculer le
rayon du cercle
circonscrit à un triangle dont on connait les trois côtés.
Caractéristiques du triangle {13, 14, 15} |
||
|
|
Sommaire de cette page >>> Triangle dans le cercle >>> Formule générale >>> Triangles en rayons entiers |
Débutants Glossaire |
|
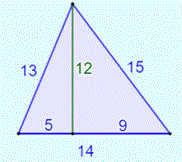
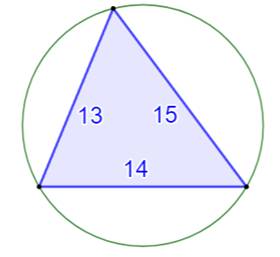
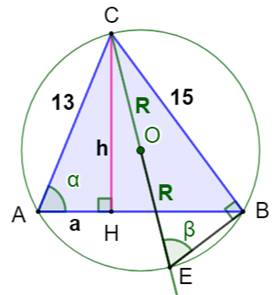
Construction Un triangle dont les côtés mesurent 13, 14 et 15
cm. Quel est le rayon du cercle circonscrit ? Voir Triangle
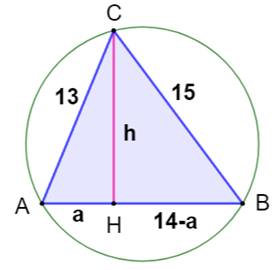
{13, 14, 15} et sa résolution Pistes Tracer un diamètre à partir de l'un des sommets
et du même sommet, tracer une hauteur. 1)
théorème
de Pythagore dans le triangle rectangle formé par la hauteur 2)
théorème
des triangles semblables pour comparer
la longueur du diamètre à des mesures connues. |
Rayon ?
|
|
|
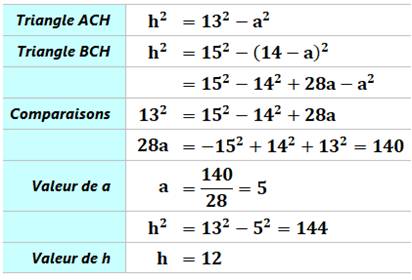
1) Calcul
de la hauteur
|
|
|
|
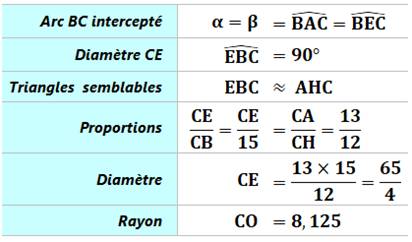
2) Calcul
du diamètre (et du rayon CO)
|
|
|
|
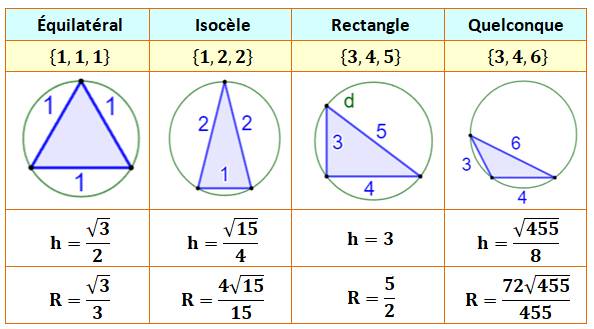
Formules Les mesures des côtés sont x, y et z avec z
le plus grand. Calcul de h puis de R:
Note: l'inégalité
triangulaire doit être satisfaite. Exemple
|
|
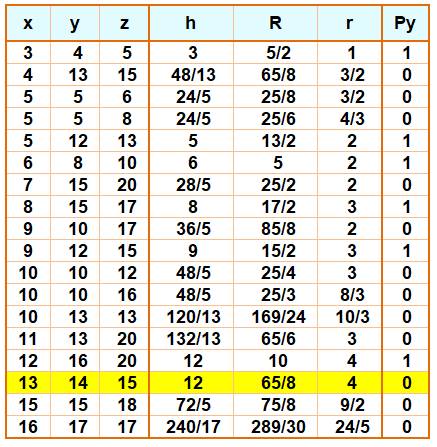
Triangles de côtés x, y et z
entiers Avec hauteur h, rayon circonscrit R et rayon
inscrit r rationnels. Py = 1 indique que le triangle est rectangle.
|
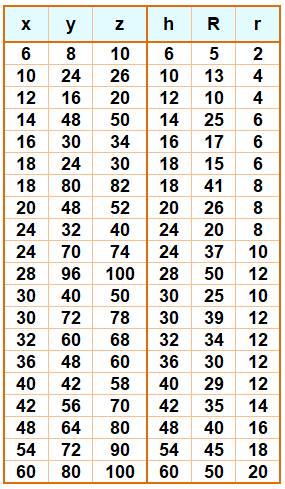
Triangles de côtés x, y et z
entiers Avec hauteur h, rayon circonscrit R et rayon
inscrit r entiers. Ils sont tous rectangles.
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/TrgCercl.htm
|