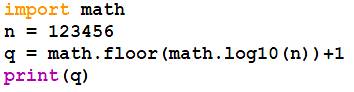|
||||||||||||||||||||||||||||||||
![]()
|
PROGRAMMATION PYTHON – PALINDROME Programmes pour débutants avec comme exemple la
recherche de palindromes:
|
|
|
Idée:
poursuivre mon apprentissage Python, en commençant tout de suite avec des
résultats concrets. Note: vous
pouvez aussi consulter d'excellents tutoriels qui vous feront
faire, pas à pas, le parcours des subtilités du langage Python. |
Remarque: Python,
comme tous les langages informatiques, à prévu l'identification des
palindromes en une seule instruction. Toute cette page est à considérer comme
un exercice d'apprentissage du langage. Programme minimal: def est_palindrome
(mot) return mot
== mot [ : : –1] Accès direct à
programmes d'identification des palindromes:
|
Voir absolument Mon espace de travail
en Python
|
|
||
|
|
Éditer Ouvrir une feuille d'édition avec CTRL N
(ou dans l'onglet Files)
Exécuter (interpréter) Lancer l'exécution du programme avec la touche F5 (ou l'onglet Run). Suite à l'instruction print, l'interpréteur affichera le logarithme
de 123456 avec 16 chiffres significatifs. |
|
|
|
||
|
|
Rappel La quantité
de chiffres d'un nombre est:
Éditer
Exécuter
|
|
|
|
Idem avec regroupement des deux instructions mathématiques en une
seule. |
|
Voir Méthode
plus simple avec longueur de chaine
|
|
||
|
Attention: avec for i in (1,10)
la boucle ne donne à i que les valeurs 1 et 10. Avec for
i in range (1,10),
alors i prend bien toutes les valeurs de 1 à 9 (10 non inclus). |
Un boucle (for)
est introduite avec i qui démarre à la
valeur de q et s'arrête à -1, en
décroissant de 1 à chaque fois (q, -1, -1) La division modulo
s'applique à deux nombres: le nombre à diviser
et son diviseur, ici les puissances
de 10 décroissantes. Puissance notée avec ** L'instruction récupère deux nombres: le quotient
et le reste (le langage Python désigne ce
couple comme étant un tuple (liste
immuable). L'itération (= répétition) de boucle met ainsi à
jour le nombre à diviser (123456, puis 23456, 3456 …) On demande l'impression du quotient d. En cartouche, le résultat de l'impression: les
chiffres de 123456, les uns après les autres. |
|
|
|
Comment obtenir la liste des chiffres d'un nombre
? Avec append qui ajoute (appose) d à la liste excitante. Attention: on écrit: L.append(d) et non pas: L
= L.append(d) L'affectation à L est automatique. |
|
Nomenclature de la boucle en Python

|
|
||
|
|
On forme une copie de A en B avec cette étrange
formalisme A[:] qui veut dira que B prend
toutes les valeurs incluses dans A, jusqu'à la fin de la liste. On utilise la méthode (= instruction) reverse (on se
souvient que la valeur est remise automatiquement dans B, sans avoir à
préciser). Attention: A = B ne copie pas la liste, mais donne deux
noms à la même liste. |
|
|
|
||
|
|
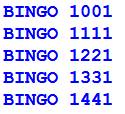
On reprend le programme qui isole les chiffres et
les place dans la liste L. Et cela pour chacun des nombres (boucle for) de 1000 à 1500 (exemple) On crée R, une copie de L, de manière à la
retourner. On teste l'égalité entre la liste des chiffres et
la liste retournée. Notez le symbole
"==" pour tester l'égalité. En cas d'égalité, imprimer le nombre palindrome. |
|
|
|
Créer la liste des palindromes. À partir du programme précédent, modifiez la fin. La liste P devient la liste P à laquelle on
ajoute (append) la valeur m. Attention: P ne peut être
modifiée que si elle existe. En tout début de programme on ajoutera: P = [ ], affectation d'une liste vide à la
variable P. |
|
|
|
||
|
|
Il est possible de tester si un nombre est palindrome
sans le module mathématique, en fait, par simple utilisation de la division
et création progressive du nombre retourné. Pas de difficulté particulière. Division
euclidienne en Python: Reste: u est l'unité de nn calculé avec le reste de la
division par 10 (nn%10). Quotient: nn est le quotient de la division par 10 de nn (nn//10). |
|
|
|
On en profite pour montrer comment demander à
l'opérateur de saisir lui-même un nombre. Le programme est identique, sauf: Le début est modifié pour entrer (input)
un nombre entier (int) au clavier. |
|
|
|
||
|
|
Dans cet exemple, on montre comment combiner plusieurs
conditions: le nombre est palindrome ET aussi un carré. Programme précédent avec: Une boucle d'exploration des nombre n Un test complémentaire: le nombre est palindrome ET
(and) carré. Test si carré: on prend la partie entière (int) de la racine carrée (sqrt) de n et on élève au carré (**2). Si ce nombre est égal à n, c'est que la
racine de n est entière. |
|
|
Le
traitement de cet exemple couvre pratiquement tout ce qu'il faut savoir pour
entreprendre la programmation Python:
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()