|
||||||||||||||||||||||||||||||||
![]()
|
PROGRAMMATION PYTHON – Arithmétique Mes premiers programmes en arithmétique avec
Python. Occasion de découvrir
quelques subtilités du langage par l'expérimentation. |
Voir absolument Mon espace de travail
en Python
|
|
||
|
Programme dans l'éditeur
Affichage dans l'interpréteur
|
But Trouver tous les diviseurs d'un nombre entier n. Exemple 1, 2, 3, 4, 6 et 12 sont diviseurs de 12 Principe Exploration des nombres successifs i de 1 à n et
test si ce nombre i divise n. Un nombre n est divisible par i si le reste de la
division est nul. Commentaires La première instruction permet de donner un
nombre entier. Input donne la main pour taper ce nombre qui est compris comme
une chaine de caractères. L'instruction int (integer = nombre en anglais)
transforme cette chaine en nombre. Lancement d'une boucle qui s'arrête à n en lui
commandant n+1. Si le reste de la division (n%i) est nul,
imprimer n. Résultat Ici, on a tapé 60 après l'invitation : nombre. Le programme lancé (run) donne la liste des diviseurs de 60. |
|
|
|
||
|
Programme dans l'éditeur
Affichage dans l'interpréteur
|
But Trouver le quotient de la division de a par b.
Annoncer également le reste. Exemple 100 / 12 = 8 reste 4. 100 / (–4) = –25 reste 0 Principe Soustraire le diviseur (b) du dividende (a)
autant de fois que la soustraction est possible. Commentaires On définit la fonction division
avec deux arguments (dividende et diviseur). On traite le signe en premier et, ceci fait, on
ne conserve que la valeur absolue (abs)
des deux nombres. Notez l'antislash
qui permet de continuer l'instruction sur la ligne suivante. Le quotient
est en fait un compteur de soustractions, mis à zéro au départ. Tant que (while)
le dividende reste plus grand que le diviseur, on soustrait et on ajoute un
au compteur-quotient. Le dernier dividende calculé est égal au reste de
la division La fonction nous transmet (return) le quotient trouvé assorti du signe,
puis le reste. Le programme principal exécute les deux exemples
de divisions. |
|
|
|
||
|
Programme dans l'éditeur
Affichage dans l'interpréteur
|
But Trouver le PGCD de deux
nombres selon l'algorithme
d'Euclide Exemple PGCD (1000, 22) = 2 Principe Algorithme d'Euclide. Commentaires On trouve ici de nombreux symboles dont la
signification est expliquée en Bases Python. On définit la fonction pgcd(a,b) qui retourne la
variable mini qui en fin de boucle vaut le pgcd. Le programme principal introduit le dialogue au
clavier. Tant que la variable encore vaut o (on a pris la précaution
de l mettre à cette valeur avant de commencer), demander deux nombres dont la
frappe sera placée en N et M. Impression d'une expression alternant du texte et
les variables N, M et le pgcd. |
|
|
|
||
|
Programme dans l'éditeur
Affichage dans l'interpréteur
|
But Trouver si un nombre est premier. Le programme
retourne 0 si n est premier, sinon il indique le facteur le plus petit. Principe Tout d'abord, on détecte si le nombre est pair,
alors on retourne 2. Sinon on examine les diviseurs impairs jusqu'à ce que
leur carré dépasse n. Si aucune divisibilité n'est trouvée, on retourne
0; le nombre est premier Notes Astuce pour détecter si un nombre
est pair: on utilise n en binaire que l'on compare à 1: Pour savoir si n est divisible par i, on teste si
son modulo (n % i) est nul. Test Le nombre 1999 produit 0, il est premier Le nombre 1234567 produit 127, il composé et
divisible par 127. |
|
|
Programme optimisé
|
But Accélérer la recherche (sans aller chercher les algorithmes
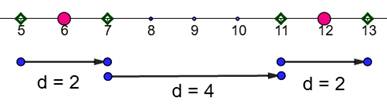
avancés de la théorie des nombres) Principe Utiliser la barre magique des nombres premiers. Elle dit que les
nombres premiers ne sont
seulement qu'en 6n
Programme Le programme élimine d'abord les cas n = 2, n =
3, n divisible par 2 et n divisible par 3. Il traite ensuit les nombre à partir de i = 5 et jusqu'à ce que le carré de i dépasse ou égale n. La boucle incrémente i
de la valeur d qui prend
alternativement les valeurs 2 puis 4. Si aucune divisibilité n'est trouvée, le
programme renvoie "True" qui
signifie que le nombre est premier. Le programme principal analyse, par exemple, la
plage des nombres de 1008 à 1015 (non compris). |
|
|
|
||
|
Algorithme
Programme dans l'éditeur
Affichage dans l'interpréteur
|
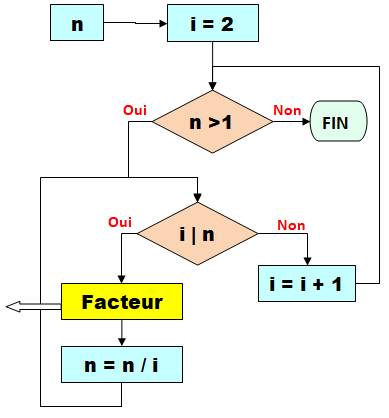
But Lister tous les facteurs
d'un nombre. Facteur = diviseurs premiers. Description de l'algorithme La variable n
est le nombre à factoriser. Lorsqu'un diviseur (i)
sera trouvé, elle prendra la valeur du quotient (n
/ i). Lorsque les divisions successives conduiront à n = 1, alors la factorisation sera terminée (boucle de
droite). Si i divise n (symbole barre verticale), on retient le
facteur et on met à jour n avec le
quotient. L'analyse continue avec le même diviseur (i) tant que le quotient (n) est divisible: détection des facteurs multiples. Après épuisement le diviseur (i) est incrémenté (boucle de
gauche) et on recommence les tests de divisibilité. Exemple (trace des variables) n = 50 /
25 5 / 1 / Fin i = 2 / 3 / 4
/ 5 / 5 Programme Préparation d'une liste avec le facteur 1. Boucle d'analyse en i
(diviseur), incrémenté en fin de boucle Boucle interne qui cherche si n est divisible par i
et combien de fois. En cas de divisibilité, le diviseur (i) est un facteur; il est ajouté (append) à a liste L. Le programme affiche tous les facteurs, même les
multiplicités, dans l'ordre croissant Avec 211 = 2 048, on a bien la liste
des onze facteurs 2. |
|
|
|
||
|
Programme dans l'éditeur
Affichage dans l'interpréteur
|
But Lister tous les facteurs
d'un nombre: chaque facteur étant associé à sa multiplicité, comme: Programme Le même que ci-dessus. À chaque passage dans la boucle interne (de
détermination de multiplicité), on incrémente un compteur (kt). En sortie de boucle, si le compteur n'est pas
nul, on ajoute le couple facteur /quantité (i et
kt) dans la liste. Format de sortie Cette fois, on traduit le fait que: 1 765 400
= 1 x 23 x 52 x 7 x 13 x 97 ou 2 048 = 1 x 211 |
|
![]()
|
|
||
|
Programme dans l'éditeur
Affichage dans l'interpréteur
Note Avec Maple,
divisors(100) produit directement la liste des
diviseurs. Python ne dispose pas de ces fonctions arithmétiques (sauf
adjonction de packages spéciaux). |
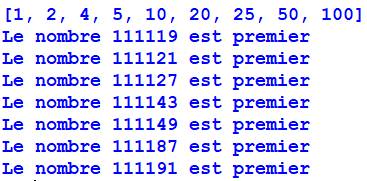
But Trouver tous les diviseurs d'un nombre n. Diviseurs Les diviseurs
vont par paire: 100 = 2 x 50 = 4 x 25
= 5 x 20 = 10 x 10 Moralité: à chaque division, on trouve deux
diviseurs et, on peut arrêter l'exploration à racine de n (10 pour 100) Commentaires On définit d'abord la recherche de diviseurs.
Ceux-ci seront placés dans la liste D. Boucle d'exploration de 1 à racine de n
(puissance 0,5 avec ** pour puissance). Divisibilité testée avec: modulo
(symbole %) nul. Le diviseur i et le quotient entier (n // i) sont ajoutés (apposés, append) à la liste déjà constituée Retour demandé en supprimant les doublons (set) et en triant les nombres (sorted) |
|
|
Solution rapide avec ensemble des
diviseurs
|
Exemple pour la concision d'écriture, mais pas
pour la rapidité de calcul Définition d'une fonction Ediv (ensemble des
diviseurs). Renvoyer k pour tous les k de 1 à n tel que k
divise n. Les accolades {…} caractérisent un ensemble:
valeurs non répétées. Attention: Python renvoie les valeurs dans un ordre
quelconque. |
|
|
Une manière raccourcie pour créer
une liste (en rouge)
|
Limitation de la recherche à la racine carrée de
n + 1, prise en nombre entier (int). Si n est divisible par k (vaut 0 mod k),
compléter l'ensemble E (c'est ce que veut dire la barre verticale suivie de
=; la barre verticale est obtenue avec Alt Gr 6)
par k et son complémentaire n//k. Le
double // donne le quotient, un nombre entier. Vous noterez que les diviseurs vont par paires: 3
x 4115 = 5 x 2469 = 15 x 823 = 12345, d'où
k et n/k |
|
|
|
||
|
Programme dans l'éditeur
Note: l'antislash
\ permet d'aller à la ligne suivante Affichage dans l'interpréteur
|
But Mettre la formation d'une liste conditionnelle en
une seule ligne. Exemple avec liste des carrés des nombres pairs Commentaires Les couple à placer dans la liste S sont n et son
carré n**2; Et, cela de n = 1 à
10, non compris; À condition que n soit un nombre pair: vaut 0 modulo 2
(le reste de la division par 2 est nul). Impression de cette liste triée (sorted). |
|
|
|
||
|
|
But Reprise du programme diviseurs, en utilisant la
forme compactée vue ci-dessus. Commentaires Apple du module math
pour calculer la racine carrée (sqrt)
plutôt que la puissance ½. D, la liste (présence des crochets [ ]) des diviseurs est calculée en une seule
ligne (imprimée sur trois avec les \ de
retour à la ligne). |
|
|
|
But Convertir la liste imbriquée de paires de nombres
en une liste unique. Commentaires Le programme précédent est complété par celui-ci. Définition de liste unique (ListUn) Tant que le programme rencontre une liste
interne, il recommence (récursivité). Sinon, il ajouté (append)
le nombre à la liste en cours de formation (DD). Impression de la liste triée (sorted). |
|
|
|
Autre
version pour les diviseurs et recherche des nombres
premiers Particularités: Déclaration d'un ensemble avec set Utilisation de la barre
verticale qui réunit les listes; ici, on ajoute k et le quotient de n
divisé par k (//) à la liste existante LD. La fonction Premier
retourne True ou False
(Vrai ou Faux) selon que la quantité de diviseurs est égale à 2 ou non,
caractérisation d'un nombre premier. Le programme principal demande les
diviseurs de 100 triés (sorted) puis, la
liste des nombres premiers dans l'intervalle demandé. |
|
À
l'occasion de l'apprentissage du langage Python, nous avons revu comment
faire la recherche des nombres premiers et,
d'une manière générale, comment établir la liste des facteurs
et des diviseurs d'un nombre. Il
existe des modules de traitement mathématique qui offre ces fonctions et
d'autres (Sympy, logiciel
libre, semble le meilleur actuellement
– Je n'ai pas encore testé; j'utilise Maple ou Maxima) |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()