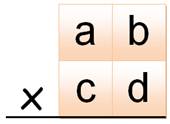|
|||||||||||||||||||||||||||||||||||||||||||
![]()
|
Multiplications à 2 x 2
chiffres Multiplications à deux
chiffres par deux chiffres. On se propose de trouver quelles sont les
multiplications à deux chiffres qui présentent le maximum de chiffres
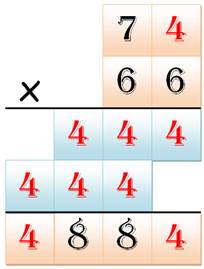
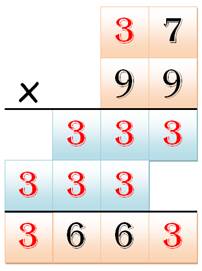
identiques, y compris dans les produits intermédiaires. Deux détiennent le
record de 9 chiffres identiques. Par ailleurs, aucune ne
donne un produit formé de quatre chiffres identiques. Mais, elles sont
nombreuses à produire trois chiffres identiques comme 31x36 = 116 ou 31x43 =
1333. |
|
|
||
|
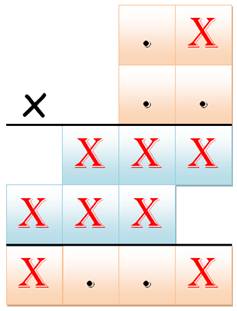
Puzzle
n°1
|
|
|
|
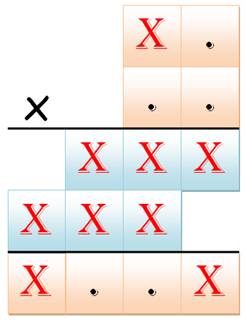
Puzzle
n°2
Ce sont les deux seules multiplications à
deux chiffres qui produisent ce record de 9 chiffres identiques. |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
n, m, P1, P2, R, 37, 33, 111, 111, 1221 19, 69, 171, 114, 1311 37, 66, 222, 222, 2442 74, 33, 222, 222, 2442 51, 55, 255, 255, 2805 37, 99, 333, 333, 3663 61, 66, 366, 366, 4026 74, 66, 444, 444, 4884 91, 55, 455, 455, 5005 86, 88, 688, 688, 7568 99, 91, 99, 891, 9009 |
|
|
|
||
|
|
67, 35, 335, 201, 2345 48, 72, 96, 336, 3456 54, 64, 216, 324, 3456 96, 36, 576, 288, 3456 97, 56, 582, 485, 5432 73, 93, 219, 657, 6789 89, 86, 534, 712, 7654 59, 23, 177, 118, 1357 |
|
|
|
||
|
La variable a varie de 1 à 9 => 9
possibilités. La variable b varie de 0 à 9 =>
10 possibilités. La variable c varie de 1 à 9 => 9
possibilités. La variable d varie de 1 à 9 => 9
possibilités. Chaque variable évoluant
indépendamment l'une de l'autre, la quantité totale de possibilité est le
produit des possibilités individuelles: Q = 9 x 10 x 9 x 9 = 7 290
Exemple: pour 17, le produit juste
inférieur à 1000 est 17 x 58 = 986
T = 7 290 – 1 294 = 5 996 |
n, m,
Q 10, 99,
81 11, 89,
72 12, 83,
66 13, 76,
60 14, 71,
55 15, 66,
51 16, 62,
47 17, 58,
44 18, 55,
41 etc. Somme cumulée sur Q 81 + 72 + 66 + … = 1 294 |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()
|
|
||
|
Puzzle
n°1
|
|
|
|
Puzzle
n°2
|
|
|